题目内容
 22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.求证:PC是⊙O的切线.
分析:连接CO,则OC=OB,所以∠B=∠OCB,根据弦切角定理得∠BAC=∠BCP,由AB直径知:∠BAC+∠B=90°,所以∠BCP+∠OCB=90°
从而证得结论.
从而证得结论.
解答:证明:连接CO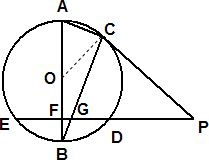
∵OC=OB,
∴∠B=∠OCB,
∵AB是直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
∵∠BAC=∠BCP,
∠BCP+∠OCB=90°,
即∠OCP=90°,
∴OC⊥PC,
∴PC是⊙O的切线.

∵OC=OB,
∴∠B=∠OCB,
∵AB是直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
∵∠BAC=∠BCP,
∠BCP+∠OCB=90°,
即∠OCP=90°,
∴OC⊥PC,
∴PC是⊙O的切线.
点评:本题考查了切线的判定方法、圆周角定理、切割线定理,是一道有关圆的综合题,有一定挑战性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
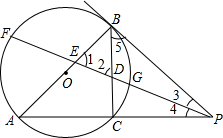 、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.
、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根. (2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E.
(2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E. 已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.
已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长. ,求∠A的度数.
,求∠A的度数.