题目内容
如图，点M是反比例函数
（
）图象上任意一点，AB⊥y轴
于B，点C是x轴上的动点，则△ABC的面积为( )
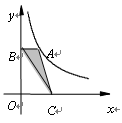
（）图象上任意一点，AB⊥y轴于B，点C是x轴上的动点，则△ABC的面积为( )
| A．1 | B．2 |
| C．4 | D．不能确定 |
A
考点：
分析：设A的坐标是：（m，n）．则n=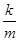
，即mn=2，根据三角形的面积公式即可求解．
解答：解：设A的坐标是：（m，n）．则n=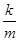，即mn=2，
∵AB=m，AB边上的高是n．
∴S△ABC=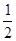
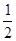mn=×2=1，
故答案是：A．
点评：主要考查了反比例函数y=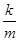中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
分析：设A的坐标是：（m，n）．则n=
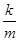，即mn=2，根据三角形的面积公式即可求解．解答：解：设A的坐标是：（m，n）．则n=
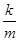，即mn=2，∵AB=m，AB边上的高是n．
∴S△ABC=
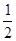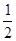mn=×2=1，故答案是：A．
点评：主要考查了反比例函数y=
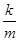中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
练习册系列答案
相关题目
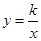经过点（2 ，―3），则k = ；
.
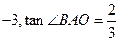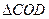的面积.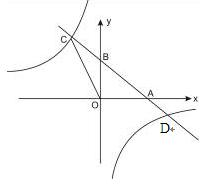
的图象的交点．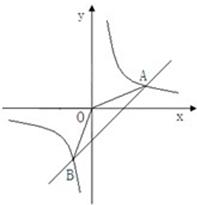
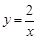，下列说法正确的是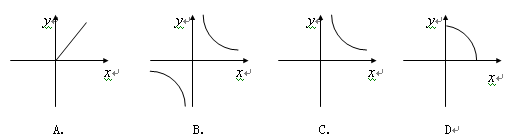
（1，m），P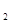
（2，n）在反比例函数 y=
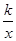（ k＞0)的图象上，则m n（填“＞”、“＜”或“=”号）
的图象位于第一、第三象限，则k的取值范围是 ( )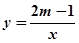
的图象的两个分支分别别位于第二、四象限，则m的取值范围是____________________.