题目内容
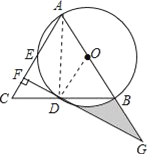
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)详见解析;(2)
【解析】(1)连接AD、OD,由AB为直径可得出点D为BC的中点,由此得出OD为△BAC的中位线,再根据中位线的性质即可得出OD⊥DF,从而证出DF是⊙O的切线;
(2)CF=1,DF=![]() ,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
(1)证明:连接AD、OD,如图所示.
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:在Rt△CFD中,CF=1,DF=![]() ,
,
∴tan∠C=![]() =
=![]() ,CD=2,
,CD=2,
∴∠C=60°,
∵AC=AB,
∴△ABC为等边三角形,
∴AB=4.
∵OD∥AC,
∴∠DOG=∠BAC=60°,
∴DG=ODtan∠DOG=2![]() ,
,
∴S阴影=S△ODG﹣S扇形OBD=![]() DGOD﹣
DGOD﹣![]() πOB2=2
πOB2=2![]() ﹣
﹣![]() π.
π.
“点睛”本题考查了等腰三角形的性质、切线的判定、扇形面积的计算以及三角形面积的计算,解题的关键是:(1)证出OD⊥DF;(2)利用分割图形求面积求出阴影部分的面积.本题属于中档题,难度不大,解决该题型题目时,利用分割图形求面积法是解题的难点,在日常练习中应加强训练.

【题目】某市现有两种用电收费方法:
分 时 电 表 | 普通电表 | |
峰时(8:00—21:00) | 谷时(21:00到次日8:00) | 电价0.52元/度 |
电价0.55元/度 | 电价0.35元/度 | |
小明家所在的小区的电表都换成了分时电表,根据情况回答下列问题:
(1)第一季度小明家用电情况为:谷时用电量100度,峰时用电量300度,这个季度的费用和用普通电表收费相比,哪种收费方法合算?试说明理由.
(2)一月份小明家用电100度,那么小明家使用分时电表是不是一定比普通电表合算?试说明理由.