题目内容
某商店经营两种业务,经营第一种业务获利y1(万元)与投资额x(万元)关系如图(1),经营第二种业务获利y2(万元)与投资额x(万元)关系如图(2),
(1)求出y1,y2关于x的关系式.
(2)若这位商家共投资10万元经营这两种业务,如你安排投资,使两种业务的总获利最大?最大值是多少?
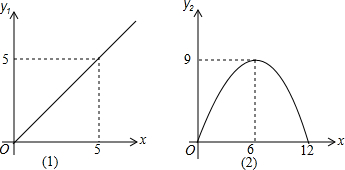
(1)求出y1,y2关于x的关系式.
(2)若这位商家共投资10万元经营这两种业务,如你安排投资,使两种业务的总获利最大?最大值是多少?
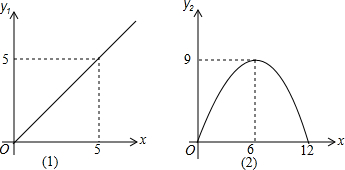
考点:二次函数的应用
专题:优选方案问题,待定系数法
分析:(1)设y1=kx,代入点(5,5)求得函数解析式;y2=a(x-6)2+9,代入点(0,0)求得函数解析式即可;
(2)设投资第一种业务m万元,则投资第二种业务为(10-m)万元,设总获利为z万元,列出二次函数求得最大值即可.
(2)设投资第一种业务m万元,则投资第二种业务为(10-m)万元,设总获利为z万元,列出二次函数求得最大值即可.
解答:解:(1)设y1=kx,代入点(5,5),解得k=1,
∴y1=x;
y2=a(x-6)2+9,代入点(0,0),解得a=-0.25,
∴y2=-0.25(x-6)2+9;
(2)设投资第一种业务m万元,则投资第二种业务为(10-m)万元,设总获利为z万元,
则z=m-0.25(10-m-6)2+9
=-0.25m2+3m+5
=-0.25(m-6)2+14;
当m=6时,z的最大值为14;
所以资第一种业务6万元,则投资第二种业务为4万元,两种业务的总获利最大,最大值是14万元.
∴y1=x;
y2=a(x-6)2+9,代入点(0,0),解得a=-0.25,
∴y2=-0.25(x-6)2+9;
(2)设投资第一种业务m万元,则投资第二种业务为(10-m)万元,设总获利为z万元,
则z=m-0.25(10-m-6)2+9
=-0.25m2+3m+5
=-0.25(m-6)2+14;
当m=6时,z的最大值为14;
所以资第一种业务6万元,则投资第二种业务为4万元,两种业务的总获利最大,最大值是14万元.
点评:此题考查待定系数法求函数解析式,二次函数的运用,以及利用配方法求函数的最大值.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,AB为一直线,OD是∠AOC的平分线,OE在∠BOC内,且∠BOE=
如图,AB为一直线,OD是∠AOC的平分线,OE在∠BOC内,且∠BOE=