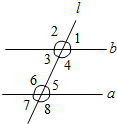题目内容
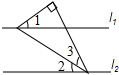
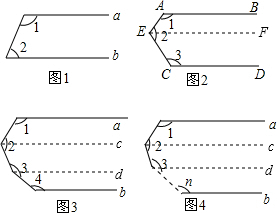
(1)如图1,a∥b,则∠1+∠2=______
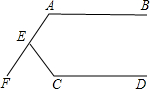
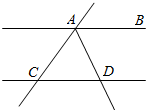
(2)如图2,AB∥CD,则∠1+∠2+∠3=______,并说明理由
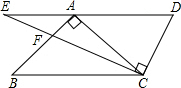
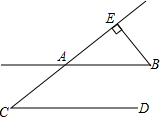
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=______
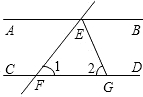
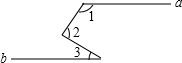
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n=______(直接写出你的结论,无需说明理由)

(2)如图2,AB∥CD,则∠1+∠2+∠3=______,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=______
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n=______(直接写出你的结论,无需说明理由)

(1)∵a∥b,
∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,
∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n-1)•180°.
故答案为:180°;360°;540°;(n-1)•180°.
∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,
∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n-1)•180°.
故答案为:180°;360°;540°;(n-1)•180°.


练习册系列答案
相关题目