题目内容
【题目】如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )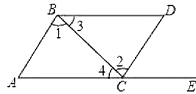
A.∠3=∠A
B.∠l=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180
【答案】B
【解析】解:A、∠3与∠A是四条线构成的角,不符合平行线的判定中的三线八角,故A不符合题意;
B、∠l与∠2是直线AB,CD被直线BC所截得内错角,根据平行线的判断方法,内错角相等二直线平行,从而得出AB∥CD,故B符合题意;
C、∠D与∠DCE是直线BD,AC被直线CD所截得内错角,根据平行线的判断方法,内错角相等二直线平行,从而得出BD∥AC,故C不符合题意;
D、∠D与∠ACD是直线BD,AC被直线CD所截得同旁内角,根据平行线的判断方法,同旁内角互补二直线平行,从而得出BD∥AC,故D不符合题意;
故应选:B 。
【考点精析】掌握平行线的判定是解答本题的根本,需要知道同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?