��Ŀ����
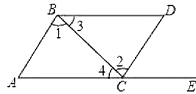
����Ŀ����֪��ͼ����COD=90����ֱ��AB��OC���ڵ�B����OD���ڵ�A������OE������AF���ڵ�G��

��1����OEƽ����BOA��AFƽ����BAD����OBA=30��������OGA= .
��2������GOA=![]() ��BOA����GAD=
��BOA����GAD=![]() ��BAD����OBA=30��������OGA= .
��BAD����OBA=30��������OGA= .
��3������2��������OBA=30�㡱��Ϊ����OBA=�����������������䣬����OGA= ���ú����Ĵ���ʽ��ʾ��
��4����OE����BOA�ֳ�1��2�����֣�AFƽ����BAD����ABO=����30��������90����������OGA�Ķ������ú����Ĵ���ʽ��ʾ��
���𰸡���1��15������2��10������3��![]() ������4��
������4��![]() ��+15����
��+15����![]() ��-15����
��-15����
��������
�����������1��������BAD=��ABO+��BOA=��+90������AFƽ����BAD�õ���FAD=![]() ��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90��������OGA=
��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90��������OGA=![]() ����Ȼ�����=30��������㼴�ɣ�
����Ȼ�����=30��������㼴�ɣ�
��2��������GOA=![]() ��BOA=30������GAD=
��BOA=30������GAD=![]() ��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90��������OGA=
��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90��������OGA=![]() ����Ȼ�����=30��������㣻
����Ȼ�����=30��������㣻
��3���ɣ�2���õ���OGA=![]() ����
����
��4�����ۣ�����EOD����COE=1��2ʱ��������BAD=��ABO+��BOA=��+90������FAD=��EOD+��OGA�õ�2��30��+2��OGA=��+90��������OGA=![]() ��+15����
��+15����
����EOD����COE=2��1ʱ������EOD=60����ͬ������OGA=![]() ��-15����
��-15����
�����������1��15����
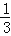
��2��10����
��3��![]() ����
����
��4������EOD����COE=1��2ʱ��
����EOD=30����
�ߡ�BAD=��ABO+��BOA=��+90����
��AFƽ����BAD��
���FAD=![]() ��BAD��
��BAD��
�ߡ�FAD=��EOD+��OGA��
��2��30��+2��OGA=��+90����
���OGA=![]() ��+15����
��+15����
����EOD����COE=2��1ʱ������EOD=60����
ͬ���õ���OGA=![]() ��-15����
��-15����
����OGA�Ķ���Ϊ![]() ��+15����
��+15����![]() ��-15����
��-15����