Question

1． （本题满分10分）如图，⊙O的直径AB＝4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．

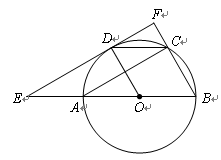
1.（1）求证：EF是⊙O的切线；

2.（2）求DE的长．

 

Answer 1

 

1.(1)证明：∵AB是⊙O的直径，

∴∠ACB＝90°．  …………………………  1分

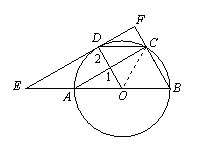∵四边形OBCD是菱形，

∴OD//BC．

∴∠1＝∠ACB＝90°．

∵EF∥AC，

∴∠2＝∠1 ＝90°．……………  2分

∵OD是半径，

∴EF是⊙O的切线

2.(2)解：连结OC，

∵直径AB＝4，

∴半径OB＝OC＝2．

∵四边形OBCD是菱形，

∴OD＝BC＝OB＝OC＝2．  …………………………………………  4分

∴∠B＝60°．

∵OD//BC，

∴∠EOD＝∠B＝ 60°．

在Rt△EOD中，

解析:略