题目内容
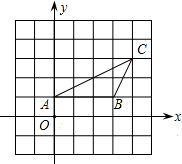
如图，平面直角坐标系中有一个边长为2的正方形AOBC，D为OB的中点，将△CBD沿直
线CD对折，点B落在点E处，连BE，过E作EF⊥OB于F．
（1）写出点C的坐标；
（2）试说明△CBD∽△BFE；
（3）求E点的坐标．
线CD对折，点B落在点E处，连BE，过E作EF⊥OB于F．（1）写出点C的坐标；
（2）试说明△CBD∽△BFE；
（3）求E点的坐标．
（1）∵OA=OB=2
∴C（2，2）（1分）
（2）设CD和BE交于点M
∵四边形AOBC是正方形
∴∠CBO=90°
∵EF⊥OB
∴∠EFB=90°
∴∠CBO=∠EFB=90°
∵CD⊥EB于点M
∴∠BCD=∠EBF（2分）
∴△CBD∽△BFE（3分）
（3）∵D是OB的中点
∴BD=
OB=1
∴在Rt△CBD中，CD=
=
=
（4分）
又∵BM是Rt△CBD斜边上的高
∴BM=
=
=
=
∴BE=2BM=2×
=
（5分）
又∵△CBD∽△BFE
∴
=
=
∴
=
=
=
∴BF=
，EF=
（6分）
∴E(
，
)（7分）
∴C（2，2）（1分）
（2）设CD和BE交于点M
∵四边形AOBC是正方形
∴∠CBO=90°
∵EF⊥OB
∴∠EFB=90°
∴∠CBO=∠EFB=90°
∵CD⊥EB于点M
∴∠BCD=∠EBF（2分）
∴△CBD∽△BFE（3分）
（3）∵D是OB的中点
∴BD=
| 1 |
| 2 |
∴在Rt△CBD中，CD=
| BC2+BD2 |
| 22+12 |
| 5 |
又∵BM是Rt△CBD斜边上的高
∴BM=
| BD•BC |
| CD |
| 1×2 | ||
|
| 2 | ||
|
2
| ||
| 5 |
∴BE=2BM=2×
2
| ||
| 5 |
4
| ||
| 5 |
又∵△CBD∽△BFE
∴
| BC |
| BF |
| BD |
| EF |
| CD |
| BE |
∴
| 2 |
| BF |
| 1 |
| EF |
| ||||
|
| 5 |
| 4 |
∴BF=
| 8 |
| 5 |
| 4 |
| 5 |
∴E(
| 2 |
| 5 |
| 4 |
| 5 |
练习册系列答案
相关题目
