题目内容
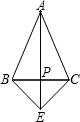 如图所示,已知AB=AC,PB=PC,下面的结论:①BE=CE;②AP⊥BC;③AE平分∠BEC;④∠PEC=∠PCE,其中正确结论的个数有
如图所示,已知AB=AC,PB=PC,下面的结论:①BE=CE;②AP⊥BC;③AE平分∠BEC;④∠PEC=∠PCE,其中正确结论的个数有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据等腰三角形的性质和全等三角形的判定与性质对各个选项进行分析,从而不难得到正确的结论.
解答:∵AB=AC,PB=PC,
∴AP⊥BC,AE平分∠BEC(三线合一),故②③正确,
∵BP=PC,∠BPE=∠CPE=90°,PE=PE,
∴△BPE≌△CPE,
∴BE=EC,故①正确,
④无法证明,
故选C.
点评:本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,难度适中.
分析:根据等腰三角形的性质和全等三角形的判定与性质对各个选项进行分析,从而不难得到正确的结论.
解答:∵AB=AC,PB=PC,
∴AP⊥BC,AE平分∠BEC(三线合一),故②③正确,
∵BP=PC,∠BPE=∠CPE=90°,PE=PE,
∴△BPE≌△CPE,
∴BE=EC,故①正确,
④无法证明,
故选C.
点评:本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
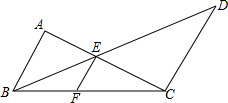 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.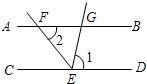 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
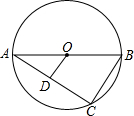 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.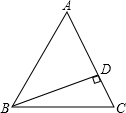 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.