题目内容
 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.分析:作AE⊥BC于E,根据等腰三角形三线合一的性质可得∠BAC=2∠CAE,且∠CAE+∠C=90°,再根据等角的余角相等即可求解.
解答: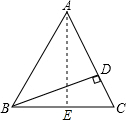 证明:作AE⊥BC于E.
证明:作AE⊥BC于E.
∵AB=AC,AE⊥BC,
∴∠BAC=2∠CAE,且∠CAE+∠C=90°,
∵BD⊥AB,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE,
∴∠BAC=2∠CBD.
 证明:作AE⊥BC于E.
证明:作AE⊥BC于E.∵AB=AC,AE⊥BC,
∴∠BAC=2∠CAE,且∠CAE+∠C=90°,
∵BD⊥AB,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE,
∴∠BAC=2∠CBD.
点评:考查了等腰三角形三线合一的性质,等角的余角相等的性质,关键是作出辅助线解答.

练习册系列答案
相关题目
 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF. 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.