Question

如图，AB是半圆O的直径，以0A为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E．则下列四个结论：
①点D为AC的中点；②S_△O′OE=

1

2

S_△AOC；③

AC

=2

AD

；④四边形O′DEO是菱形．其中正确的结论是

 

．（把所有正确的结论的序号都填上）

Answer 1

分析：①连接DO，利用园中角定理以及垂径定理求出即可；
②利用相似三角形的性质，面积比等于相似比的平方求出即可；
③利用弧长计算公式求出即可；
④根据菱形的判定得出即可．

解答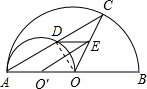：解：①连接DO，
∵AO是半圆直径，
∴∠ADO=90°，
∵OD⊥AC，
∴AD=DC，
∴①正确．
②∵O′E∥AC，
∴△EO′O∽△AOC，
∴

OO′

AO

=

1

2

，
∴S_△O′OE=

1

4

S_△AOC，
∴②错误．
③∵OD⊥AC，AD=DC，
∴∠AOD=∠DOC，
∴∠AO′D=∠AOC，
AO=2AO′，
∴

AC

=2

AD

；
∴③正确；
④∵D为AC中点，O′为AO中点，
∴DO′是△AOC中位线，
∴DO′∥CO，
∵O′E∥AC，
∴O′为AO中点，
∵D为AC中点，
∴DE∥AO，
∴四边形DO′OE是平行四边形，
∵DO′=O′O，
∴四边形O′DEO是菱形．
∴④正确．
综上所述，只有①③④正确．
故答案为：①③④．

点评：此题主要考查相似三角形的判定与性质，圆心角、弧、弦的关系，圆周角定理，等腰三角形的性质，三角形内角和定理等知识点的灵活运用，此题步骤繁琐，但相对而言，难易程度适中，很适合学生的训练是一道典型的题目．