题目内容
如图，AB是半圆O的直径，点D是半圆上一动点，AB=10，AC=8，当△ACD是等腰三角形时，点D到AB的距离是分析：此题需分两种情况，AC边为底时和AC边位腰时，求得点D到AB的距离．
解答：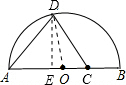
解：（1）若AC为底边时，D在以AC为边的中垂线上，如图所示：
作DE⊥AB，AB=10，AC=8，△ACD是等腰三角形，AE=EC=4，
OD=5，OE=1，则由勾股定理可得：DE=2
．
（2）当AC为△ACD的腰时，AC=AD或AC=CD，二者求得的点D到AB的距离相等．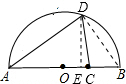
在这里只讨论一下AC=AD的情况：
如图，连接BD，作DE⊥AB，
由于AB为直径，AD⊥BD，AD=AC=8，AB=10，则BD=6．
又
AD•BD=
AB•DE，则DE=4.8．
解：（1）若AC为底边时，D在以AC为边的中垂线上，如图所示：作DE⊥AB，AB=10，AC=8，△ACD是等腰三角形，AE=EC=4，
OD=5，OE=1，则由勾股定理可得：DE=2
| 6 |
（2）当AC为△ACD的腰时，AC=AD或AC=CD，二者求得的点D到AB的距离相等．
在这里只讨论一下AC=AD的情况：
如图，连接BD，作DE⊥AB，
由于AB为直径，AD⊥BD，AD=AC=8，AB=10，则BD=6．
又
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查了相似三角形的性质及勾股定理，同学们要熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
如图，AB是半圆O的直径，AC是弦，点P从点B开始沿BA边向点A以1cm/s的速度移动，若AB长为10cm，点O到AC的距离为4cm．
已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．
如图，AB是半圆O的直径，以OA为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E，则下列结论：①S△O′OE=
