题目内容
如图,在直角梯形OABC中,CB∥OA,∠OAB=90°,点O为坐标原点,点A在x轴的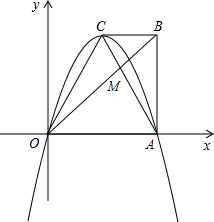 正半轴上,对角线OB,AC相交于点M,OA=AB=4,OA=2CB.
正半轴上,对角线OB,AC相交于点M,OA=AB=4,OA=2CB.(1)点C的坐标为
(2)求△OCM的面积;
(3)若点E在过O,A,C三点的抛物线的对称轴上,点F为该抛物线上的点,且以A,O,F,E四点为顶点的四边形为平行四边形,求点F的坐标.
分析:(1)由于AB为4,CB∥OA,则C点纵坐标为4,作CG⊥AO与x轴交于点G,结合OA=AB=4,OA=2CB即可得出C点坐标.
(2)根据△CMB∽△AMO,得出
=
=1:2;求出△BCM的面积为△OCM面积的一半,又根据△CBO面积为△BOA面积的一半,只要求出梯形OABC的面积即可求出△OCM的面积.
(3)先求出二次函数解析式,再根据平行四边形的性质求出F点横坐标,将横坐标代入解析式即可求出F点的纵坐标,注意,符合条件的F点不止一个.
(2)根据△CMB∽△AMO,得出
| BM |
| OM |
| BC |
| AO |
(3)先求出二次函数解析式,再根据平行四边形的性质求出F点横坐标,将横坐标代入解析式即可求出F点的纵坐标,注意,符合条件的F点不止一个.
解答: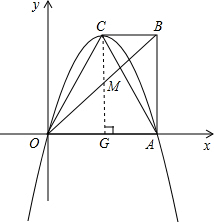 解:(1)如图,作CG⊥AO与x轴交于点G,则CB=AG,
解:(1)如图,作CG⊥AO与x轴交于点G,则CB=AG,
∵OA=2CB,
∴OA=2AG,
∵AO=4,
∴OG=2,
由于AB为4,CB∥OA,则C点纵坐标为4,
∴C(2,4).
(2)∵AO=2CB,
∴2S△CBO=S△AOB,
∵S梯形ABCO=
(CB+AO)•AB=
×(2+4)×4=12,
∴S△CBO=12×
=4,
∵CB∥AO,
∴△CMB∽△AMO,
∴
=
,
=
,
则
=
,
∴S△COM=
S△COB=
×4=
;
(3)∵O(0,0),A(4,0),C(2,4),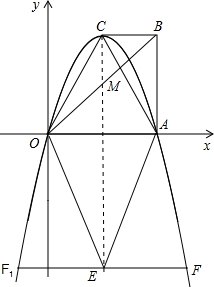
∴设解析式为y=a(x-0)(x-4),
将(2,4)代入解析式得,4=a(2-0)(2-4),
解得a=-1.
则解析式为y=-(x-0)(x-4)=-x2+4x.
由图可知F点横坐标为2+4=6,
将x=6代入y=-(x-0)(x-4)=-x2+4x得,
y=-36+4×6=-12,
故F(6,-12).
由图可知F1点横坐标为2-4=-2,
将x=-2代入y=-(x-0)(x-4)=-x2+4x得,
y=-36+4×6=-12,
故F1(-2,-12).
当F与C重合时,F2(2,4).
故F点的坐标为:(6,-12),F1(-2,-12),F2(2,4).
 解:(1)如图,作CG⊥AO与x轴交于点G,则CB=AG,
解:(1)如图,作CG⊥AO与x轴交于点G,则CB=AG,∵OA=2CB,
∴OA=2AG,
∵AO=4,
∴OG=2,
由于AB为4,CB∥OA,则C点纵坐标为4,
∴C(2,4).
(2)∵AO=2CB,
∴2S△CBO=S△AOB,
∵S梯形ABCO=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△CBO=12×
| 1 |
| 3 |
∵CB∥AO,
∴△CMB∽△AMO,
∴
| CB |
| AO |
| BM |
| OM |
| CB |
| AO |
| 1 |
| 2 |
则
| BM |
| OM |
| 1 |
| 2 |
∴S△COM=
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
(3)∵O(0,0),A(4,0),C(2,4),

∴设解析式为y=a(x-0)(x-4),
将(2,4)代入解析式得,4=a(2-0)(2-4),
解得a=-1.
则解析式为y=-(x-0)(x-4)=-x2+4x.
由图可知F点横坐标为2+4=6,
将x=6代入y=-(x-0)(x-4)=-x2+4x得,
y=-36+4×6=-12,
故F(6,-12).
由图可知F1点横坐标为2-4=-2,
将x=-2代入y=-(x-0)(x-4)=-x2+4x得,
y=-36+4×6=-12,
故F1(-2,-12).
当F与C重合时,F2(2,4).
故F点的坐标为:(6,-12),F1(-2,-12),F2(2,4).
点评:此题考查了二次函数的性质和梯形及平行四边形的性质,将坐标与图形相结合,使得这道题充分体现了数形结合的重要性,同时要注意分类讨论.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 动时间为t(单位:秒).
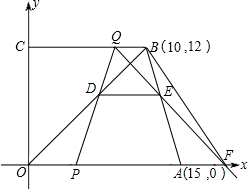
动时间为t(单位:秒).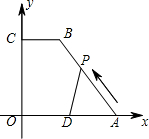 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.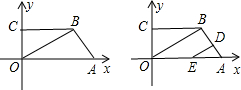
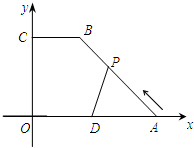 单位,移动时间记为t秒.
单位,移动时间记为t秒.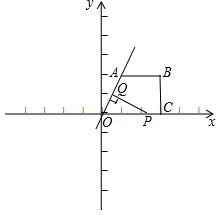 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.