题目内容
如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A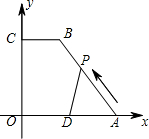 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时点P的坐标?
分析:(1)题目给出了B、C点的坐标,可设出直线BC的解析式,应用待定系数法求出解析式即可;
(2)可根据四边形OPDC的面积是梯形COAB面积,列出方程并解出方程即可;
(3)要根据P的位置在不同边的具体情况利用相关的知识写出函数关系式及取值范围.
(2)可根据四边形OPDC的面积是梯形COAB面积,列出方程并解出方程即可;
(3)要根据P的位置在不同边的具体情况利用相关的知识写出函数关系式及取值范围.
解答: 解:(1)点B坐标为(4,8),AB=
解:(1)点B坐标为(4,8),AB=
=10,(1分)
由5+t=
,得t=11.(1分)
此时点P在CB上;(1分)
(2)解法一:作OF⊥AB于F,BE⊥OA于E,DH⊥AB于H,
则BE=OC=8.
∵AE=OA-BC=10-4=6,
∴AB=
=10,
∴AB=OA,
∵OA•BE=AB•OF,
∴OF=BE=8,DH=4.(1分)
∴S=
×4×t=2t(0<t<10);(1分)
解法二
∵
=
,∴
=
,(1分)
即S=2t(0<t≤10);(1分)
(3)点P只能在AB或OC上,
(ⅰ)当点P在AB上时,设点P的坐标为(x,y).
由S△APD=
S梯形COAB,
得
×5×y=14,得y=
,
此时t=7.
由(10-x)2+(
)2=49,得x=
.
即在7秒时有点P1(5
,5
);(1分)
(ⅱ)当点P在OC上时,设点P的坐标为(0,y).
由S△OPD=
S梯形COAB,
得
×5×y=14,得y=
,
此时t=14+(8-
)=16
.
即在16
秒时,有点P2(0,5
).(1分)
故在7秒时有点P1(5
,5
),在16
秒时有点P2(0,5
),使PD将梯形COAB的面积分成1:3的两部分.(1分)
 解:(1)点B坐标为(4,8),AB=
解:(1)点B坐标为(4,8),AB=| (10-4)2+(0-8)2 |
由5+t=
| 10+10+4+8 |
| 2 |
此时点P在CB上;(1分)
(2)解法一:作OF⊥AB于F,BE⊥OA于E,DH⊥AB于H,
则BE=OC=8.
∵AE=OA-BC=10-4=6,
∴AB=
| BE2+AE2 |
∴AB=OA,
∵OA•BE=AB•OF,
∴OF=BE=8,DH=4.(1分)
∴S=
| 1 |
| 2 |
解法二
∵
| S△APD |
| S△ABD |
| AP |
| AB |
| S | ||
|
| t |
| 10 |
即S=2t(0<t≤10);(1分)
(3)点P只能在AB或OC上,
(ⅰ)当点P在AB上时,设点P的坐标为(x,y).
由S△APD=
| 1 |
| 4 |
得
| 1 |
| 2 |
| 28 |
| 5 |
此时t=7.
由(10-x)2+(
| 28 |
| 5 |
| 29 |
| 5 |
即在7秒时有点P1(5
| 4 |
| 5 |
| 3 |
| 5 |
(ⅱ)当点P在OC上时,设点P的坐标为(0,y).
由S△OPD=
| 1 |
| 4 |
得
| 1 |
| 2 |
| 28 |
| 5 |
此时t=14+(8-
| 28 |
| 5 |
| 2 |
| 5 |
即在16
| 2 |
| 5 |
| 3 |
| 5 |
故在7秒时有点P1(5
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
点评:本题考查了直角梯形及一次函数的综合运用;做题时要认真理解题意,找出等量关系,而分类讨论是正确解答本题的关键.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位线EF分别交BD,AC于点G,H,∠ACB=30°,则下列结论中正确的有
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位线EF分别交BD,AC于点G,H,∠ACB=30°,则下列结论中正确的有

