Question

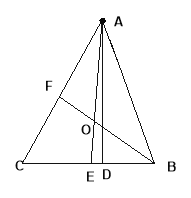
【题目】如图，点O在直线AB上，OE、OD分别是∠AOC、∠BOC的平分线.

(1)∠AOE的补角是∠____；∠BOD的余角是______；

(2)若∠AOC=118°，求∠COD的度数；

(3)射线OD与OE之间有什么特殊的位置关系？为什么？

Answer 1

【答案】（1）BOE，∠AOE和∠COE；（2）31°；（3）OD⊥OE

【解析】试题分析：

（1）根据图形结合“补角的定义”可得∠AOE的补角是∠BOE；由OE、OD分别是∠AOC、∠BOC的平分线，可得∠COE=∠AOE=∠AOC，∠COD=∠BOD=∠BOC，从而可证得∠COE+∠COD=∠DOE=90°，由此可得∠BOD+∠COE=90°，∠BOD+∠AOE=90°，从而可知，∠BOD的余角是∠AOE和∠COE；

（2）由∠AOC的度数可先求得∠BOC的度数，再由OD平分∠BOC即可得到∠COD的度数；

（3）由（1）可知∠DOE=90°，由此就可得到OE⊥OD.

试题解析：

（1）∵点O在直线AB上，

∴∠AOE+∠BOE=180°，∠AOC+∠BOC=180°，

∴∠AOE的补角是∠BOE.

∵OE、OD分别是∠AOC、∠BOC的平分线，

∴∠COE=∠AOE=∠AOC，∠COD=∠BOD=∠BOC，

∴∠COE+∠COD= (∠AOC+∠BOC)= ∠AOB=90°，

∴∠BOD+∠COE=90°，∠BOD+∠AOE=90°，

∴在图中，∠BOD的余角是∠AOE和∠COE；

（2）由（1）可知，∠AOC+∠BOC=180°，∠COD=∠BOD=∠BOC，

∴∠BOC=180°-∠AOC=180°-118°=62°，

∴∠COD=62°×=31°；

（3）射线OD与OE之间的位置关系是：OD⊥OE，理由如下：

由（1）可知：∠DOE=∠COE+∠COD= (∠AOC+∠BOC)= ∠AOB=90°，

∴OD⊥OE.