题目内容
【题目】【探索新知】
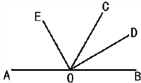
如图1,点C将线段AB分成AC和BC两部分,若BC= ![]() AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
(1)若AC=3,则AB=_____;
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC_____DB;(填“=”或“≠”)
【深入研究】
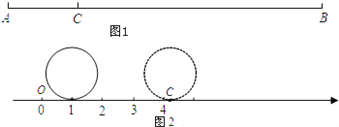
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度.
【答案】(1)![]() ;(2)=;(3)
;(2)=;(3)![]()
【解析】试题分析:
(1)由题意可知,当AC=3时,可由BC= ![]() AC先求得BC,再由AB=AC+BC可求得AB;
AC先求得BC,再由AB=AC+BC可求得AB;
(2)由题意易得:AB=AC+BC=AC+ ![]() AC=
AC=![]() AC;AB=AD+BD=
AC;AB=AD+BD= ![]() BD+BD=
BD+BD=![]() BD;由此可得AC=BD;
BD;由此可得AC=BD;
(3)由题意可知,OC= ![]() ,设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:OM
,设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:OM![]() =
= ![]() ,CN
,CN![]() =
= ![]() ,由此解得:OM=1,CN=1,所以可得MN=OC-OM-CN=
,由此解得:OM=1,CN=1,所以可得MN=OC-OM-CN= ![]() .
.

试题解析:
(1)由题意可知,当AC=3时,BC=![]() ,
,
∴AB=AC+BC=![]() ;
;
(2)由题意可知,AB=AC+BC=AC+ ![]() AC=
AC=![]() AC;
AC;
∵点D是AB上不同于点C的另一个圆周率点,
∴AB=AD+BD= ![]() BD+BD=
BD+BD=![]() BD;
BD;
∴![]() AC=
AC=![]() BD,
BD,
∴AC=BD;
(3)如图2,由题意可知:OC= ![]() .
.
设点M是线段OC靠近点O的圆周率点,点N是线段OC靠近点C的圆周率点,则由题意可得:
OM![]() =
= ![]() ,CN
,CN![]() =
= ![]() ,
,
由此解得:OM=1,CN=1,
∴MN=OC-OM-CN= ![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目