题目内容
【题目】如图,在正方形ABCD中,连接AC,点E为正方形ABCD内一点,∠BAE=∠BCE=15°,点F为AE延长线上一点,且BF=BC,连接CF,下列结论:①EF平分∠BEC;②△BCF是等边三角形;③∠AFC=45°;④EF=AE+BE.正确的是( )
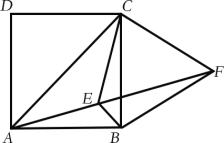
A.①②B.②③C.①②③D.①②③④
【答案】D
【解析】
利用正方形的性质,易证△ABE≌△CBE,得到∠ABE=∠CBE=45°,由三角形外角性质易得∠BEF=∠CEF=60°,所以①正确;利用BF=BC=BA,易推出∠CBF=60°,则可判定△BCF为等边三角形,所以②正确;由②的结论易得∠AFC=60°-15°=45°,所以③正确;在EF上截取FN=AE,易证△BAE≌△BFN,推出EN=BE,即可判断④.
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠BAC=∠BCA=45°,
∵∠BAE=∠BCE=15°
∴∠EAC=∠ECA=30°,
∴EA=EC,
在△ABE和△CBE中,
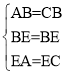
∴△ABE≌△CBE(SSS)
∴∠ABE=∠CBE=![]() ∠ABC=45°,
∠ABC=45°,
∴∠BEF=∠BAE+∠ABE=60°,
∵∠CEF=∠EAC+∠ECA=60°,
∴∠BEF=∠CEF
∴EF平分∠BEC,故①正确;
∵BF=BC=BA
∴∠BFA=∠BAF=15°,
∴∠ABF=150°,
∴∠CBF=∠ABF-∠ABC=60°,
又∵BF=BC
∴△BCF为等边三角形,故②正确;
∵△BCF为等边三角形
∴∠BFC=60°,
∴∠AFC=∠BFC-∠BFA=60°-15°=45°,故③正确;
如图所示,在EF上截取FN=AE,
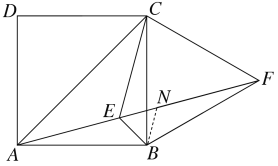
在△BAE和△BFN中,
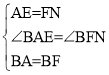
∴△BAE≌△BFN(SAS)
∴BE=BN
又∵∠BEF=60°,
∴△BEN为等边三角形,
∴EN=BE
∴EF=FN+EN=AE+BE,故④正确;
①②③④正确,故选D.

 小学教材完全解读系列答案
小学教材完全解读系列答案