Question

在矩形ABCD中，点P是边AD上的动点，连接BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，连接QP（如图）．已知AD=13，AB=5，设AP=x，BQ=y．

（1）求y关于x的函数解析式，并写出x的取值范围；
（2）当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；
（3）点E在边CD上，过点E作直线QP的垂线，垂足为F，如果EF=EC=4，求x的值．

Answer 1

解：（1）根据题意，得AP=x，BQ=y，AB=5，，
∵QM是线段BP的垂直平分线，∴。
易得△ABP∽△MQB，∴，即。
化简，得。
∴y关于x的函数解析式为，x的取值范围为。
（2）根据题意，⊙P和⊙Q的圆心距PQ="BQ=" y，⊙P的半径为，⊙Q的半径为，
若⊙P和⊙Q外切，则，即。
代入，得
解得 。
∴当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，。
（3）∵EF=EC=4，且EF⊥PQ，EC⊥BC，
∴PQ和BC是以点E 为圆心，4为半径圆的两条切线。
连接EQ，

易得，△ABP∽△CEQ，∴。
∵AB=5，AP=x，CE=4，CQ=，
∴，即。
代入，得
整理，得，解得。
∴满足条件的x值为：或。

试题分析：（1）由△ABP∽△MQB列比例式即可得y关于x的函数解析式。
当y=13时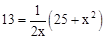，，解得，此为x的最小值；最大值为13。因此，x的取值范围为。
（2）若⊙P和⊙Q外切，圆心距等于两半径之和，据此列式化简代入（1）的函数关系式求解。
（3）根据题意，PQ和BC是以点E 为圆心，4为半径圆的两条切线，从而可得△ABP∽△CEQ，据此列比例式简代入（1）的函数关系式求解。