Question

【题目】如图，在△ABC中，BD是角平分线，且∠ACB＝60°，∠ADB＝97°，

(1)求∠A

(2) 在图中画出△ABC边AB上的高CE.并求出∠ACE的度数．

Answer 1

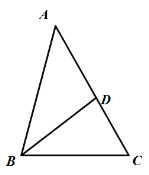
【答案】（1）∠A＝46°；(2)∠ACE＝44°.

【解析】

（1）先根据三角形外角的性质求出∠DBC的值，再由角平分线的定义求出∠ABC的值，然后根据三角形内角和即可求出∠A的值；

（2）根据高线的定义作出CE即可，然后根据直角三角形两锐角互余即可求出∠ACE的值.

（1）∵∠ADB＝∠DBC＋∠ACB，

∴∠DBC＝∠ADB－∠ACB＝97°－60°＝37°，

.∵BD是角平分线，

∴∠ABC＝74°，

∴∠A＝180°－∠ABC－∠ACB＝46°.

(2)如图，

∵CE是高，

∴∠AEC＝90°，

∴∠ACE＝90°－∠A＝44°.