题目内容
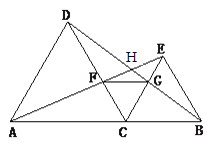
【题目】如图,C是线段AB上一点,分别以AC、CB为边作等边三角形ACD和CBE,连结AE、BD,AE交DC、DB分别为F点、H点,BD交CE于G点,连结FG.求证:① ∠FAC=∠HDC ;② ∠HFG=∠HAC;③ ∠BHA=120 °.
【答案】①证明见解析;②证明见解析;③证明见解析.
【解析】
①由“ASA”可证△ACE≌△DCB,从而可以证明∠FAC =∠HDC;
②先证明△ACF≌△DCG得CF=CG,得出△FCG是等边三角形得∠GFC=∠ACD,从而可证明FG∥AB,进而证明结论;
③证明∠DHA=∠ACD=60°即可得结论.
①∵△ACD和△BCE是等边三角形,
∴∠ACD=∠BCE=60°,AC=DC,EC=BC,
∴∠ACD+∠DCE=∠DCE+∠ECB,
即∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴∠FAC =∠HDC;
②∵∠EAC=∠BDC,
∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
∴∠ACD=∠DCG=60°,且∠EAC=∠BDC,AC=DC,
∴△ACF≌△DCG(ASA),
∴CF=CG,
∵∠FCG=60°
∴△FCG是等边三角形
∴∠GFC=∠ACD=60°,
∴FG∥AB,
∴∠HFG=∠HAC
③∵△ACE≌△DCB
∴∠CAE=∠BDC
∵∠ACD=∠BDC+∠CBD=60°
∴∠DHA=∠CAE+∠CBD=60°
∴∠BHA=120 °.

【题目】个体户小王在上周日以每千克4元买进金佛山鲜笋![]() ,进入农贸市场后共占5个摊位,每个摊位最多容纳
,进入农贸市场后共占5个摊位,每个摊位最多容纳![]() 鲜笋,每个摊位的市场管理价为每天20元,下表为本周内鲜笋每天的销售价格与前一天相比价格的涨跌情况(涨记为正,跌记为负).星期一的价格是在周日每千克4元买进价格基础上涨了1.3元.
鲜笋,每个摊位的市场管理价为每天20元,下表为本周内鲜笋每天的销售价格与前一天相比价格的涨跌情况(涨记为正,跌记为负).星期一的价格是在周日每千克4元买进价格基础上涨了1.3元.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +1.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)鲜笋销售最高价格为每千克多少元?
(2)小王在上周日以每千克4元买进金佛山解笋![]() ,进入批发市场后共占5个摊位,小王在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算?
,进入批发市场后共占5个摊位,小王在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算?