题目内容
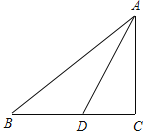
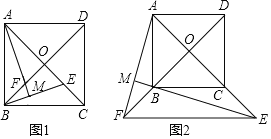
【题目】正方形ABCD的对角线AC、BD交于点O,点E、F分别在OC、OB上,且OE=OF.
(1)如图1,若点E、F在线段OC、OB上,连接AF并延长交BE于点M,求证:AM⊥BE;
(2)如图2,若点E、F在线段OC、OB的延长线上,连接EB并延长交AF于点M.
①∠AME的度数为 ;
②若正方形ABCD的边长为3![]() ,且OC=3CE时,求BM的长.
,且OC=3CE时,求BM的长.
【答案】(1)见解析;(2)①90° ;②![]()
【解析】
(1)由“SAS”可证△AOF≌△BOE,可得∠FAO=∠OBE,由余角的性质可求AM⊥BE;
(2)①由“SAS”可证△AOF≌△BOE,可得∠FAO=∠OBE,由余角的性质可求∠AME的度数;
②由正方形性质可求AC=6,可得OA=OB=OC=3,AE=7,OE=4,由勾股定理可求BE=5,通过证明△OBE∽△MAE,可得![]() ,可求ME的长,即可得BM的长.
,可求ME的长,即可得BM的长.
证明:(1)∵四边形ABCD是正方形
∴AO=BO=CO=DO,AC⊥BD
∵AO=BO,∠AOF=∠BOE=90°,OE=OF
∴△AOF≌△BOE(SAS)
∴∠FAO=∠OBE,
∵∠OBE+∠OEB=90°,
∴∠OAF+∠BEO=90°
∴∠AME=90°
∴AM⊥BE
(2)①∵四边形ABCD是正方形
∴AO=BO=CO=DO,AC⊥BD
∵AO=BO,∠AOF=∠BOE=90°,OE=OF
∴△AOF≌△BOE(SAS)
∴∠FAO=∠OBE,
∵∠OBE+∠OEB=90°,
∴∠FAO+∠OBE=90°
∴∠AME=90°
故答案为:90°
②∵AB=BC=3![]() ,∠ABC=90°
,∠ABC=90°
∴AC=6
∴OA=OB=OC=3
∵OC=3CE
∴CE=1,
∴OE=OC+CE=4,AC=AC+AE=7
∴BE=![]() =5
=5
∵∠AME=∠BOE=90°,∠AEM=∠OEB
∴△OBE∽△MAE
∴![]()
∴![]()
∴ME=![]()
∴MB=ME-BE=![]() -5=
-5=![]()

 名校课堂系列答案
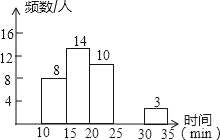
名校课堂系列答案【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?