题目内容
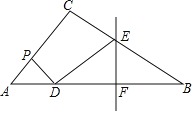
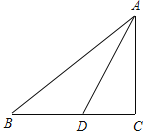
【题目】如图，△ABC中，∠C＝90°，D是BC边上一点，∠ADC＝3∠BAD，BD＝8，DC＝7，则AB的值为（ ）
A. 15 B. 20 C. 2
+7 D. 2+
【答案】B
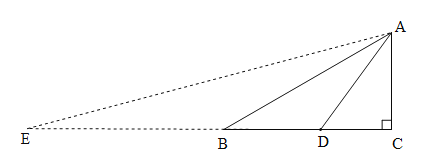
【解析】分析：延长CB到E使BE=BA，接连EA．设AB=a，则BE=a．由等腰三角形的性质和三角形外角的性质得到∠E=∠BAD，即可证明△ABD∽△EAD，由相似三角形的性质可得到AD2=8（8+a）=64+8a．在Rt△ACD和Rt△ABC中，利用勾股定理得到
，解方程即可得到结论．
详解：延长CB到E使BE=BA，接连EA．设AB=a，则BE=a．∵BE=BA，∴∠E=∠EAB，∴∠ABD=2∠E．∵∠ADC＝3∠BAD，∠ADC=∠ABD+∠BAD，∴∠ABD=2∠BAD，∴∠E=∠BAD．∵∠ADB=∠ADB，∴△ABD∽△EAD，∴BD：AD=AD：ED，∴AD2=BDED，∴AD2=8（8+a）=64+8a．在Rt△ACD中，AC2=AD2-DC2=64+8a-49=15+8a．在Rt△ABC中，∵AB2=BC2+AC2，∴，∴
，∴（a-20）（a+12）=0，解得：a=20或a=－12（舍去）．故选B．
优质课堂快乐成长系列答案【题目】某天，一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg，然后在市场上按零售价出售，西红柿和豆角当天的批发价和零售价如下表所示：
品名 | 西红柿 | 豆角 |
批发价（单位：元/kg） | 2.0 | 1.5 |
零售价（单位：元/kg） | 2.9 | 2.6 |
如果西红柿和豆角全部以零售价售出，他当天卖这些西红柿和豆角赚了多少元钱？
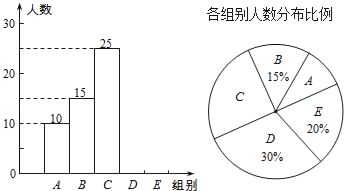
【题目】某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
组别 | 正确字数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息完成下列问题：
（1）统计表中的m＝ ，n＝ ，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是 ；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
