题目内容
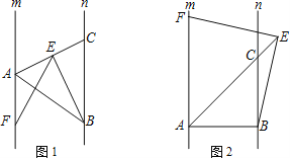
【题目】已知:直线m∥n,点A,B分别是直线m,n上任意两点,在直线n上取一点C,使BC=AB,连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)如图1,当点E在线段AC上,且∠AFE=30°时,求∠ABE的度数;
(2)若点E是线段AC上任意一点,求证:EF=BE;
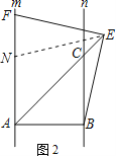
(3)如图2,当点E在线段AC的延长线上时,若∠ABC=90°,请判断线段EF与BE的数量关系,并说明理由.
【答案】(1)30°;(2)见解析;(3)EF=BE,见解析
【解析】
(1)根据平行线的性质得到∠FAB=∠ABC,根据三角形内角和定理解答即可;
(2)以点E为圆心,以EA为半径画弧交直线m于点M,连接EM,证明△AEB≌△MEF,根据全等三角形的性质证明;
(3)在直线m上截取AN=AB,连接NE,证明△NAE≌△ABE,根据全等三角形的性质得到EN=EB,∠ANE=∠ABE,证明EN=EF,等量代换即可.
(1)∵m∥n,
∴∠FAB=∠ABC,
∵∠BEF=∠ABC,
∴∠FAB=∠BEF,
∵∠AHF=∠EHB,∠AFE=30°,
∴∠ABE=30°;
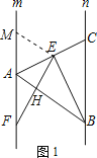
(2)如图1,以点E为圆心,以EA为半径画弧交直线m于点M,连接EM,
∴EM=EA,
∴∠EMA=∠EAM,
∵BC=AB,
∴∠CAB=∠ACB,
∵m∥n,
∴∠MAC=∠ACB,∠FAB=∠ABC,
∴∠MAC=∠CAB,
∴∠CAB=∠EMA,
在△AEB和△MEF中,
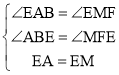 ,
,
∴△AEB≌△MEF(AAS)
∴EF=EB;
(3)EF=BE.
理由如下:如图2,在直线m上截取AN=AB,连接NE,
∵∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵m∥n,
∴∠NAE=∠ACB=∠CAB=45°,∠FAB=90°,
在△NAE和△ABE中,
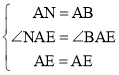 ,
,
∴△NAE≌△ABE(SAS),
∴EN=EB,∠ANE=∠ABE,
∵∠BEF=∠ABC=90°,
∴∠FAB+∠BEF=180°,
∴∠ABE+∠EFA=180°,
∴∠ANE+∠EFA=180°
∵∠ANE+∠ENF=180°,
∴∠ENF=∠EFA,
∴EN=EF,
∴EF=BE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?