题目内容
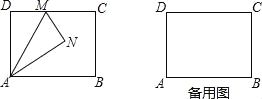
【题目】如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．
（1）当AN平分∠MAB时，求DM的长；
（2）连接BN，当DM=1时，求△ABN的面积；
（3）当射线BN交线段CD于点F时，求DF的最大值．
【答案】（1）DM=
；（2）
；（3）
．
【解析】试题分析：（1）由折叠可知：△ANM≌△ADM，∠MAN=∠DAM，由AN平分∠MAB，得到∠MAN=∠NAB，进一步有∠DAM=∠MAN=∠NAB．由四边形ABCD是矩形，得到∠DAM=30°，由DM=ADtan∠DAM得到DM的长；
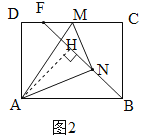
（2）如图1，延长MN交AB延长线于点Q，∵由四边形ABCD是矩形，得到∠DMA=∠MAQ．由折叠可知：△ANM≌△ADM，∠DMA=∠AMQ，得到∠MAQ=∠AMQ，故MQ=AQ．
设NQ=x，则AQ=MQ=1+x．在Rt△ANQ中，由
，得到x=4．
故NQ=4，AQ=5，由
=
=
ANNQ，即可得到结论；
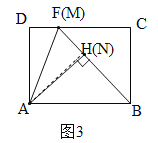
（3）如图2，过点A作AH⊥BF于点H，则△ABH∽△BFC，故
.由AH≤AN=3，AB=4，故当点N、H重合（即AH=AN）时，DF最大．此时M、F重合，B、N、M三点共线，△ABH≌△BFC（如图3），而CF=BH=
=
，故课求出DF的最大值．
试题解析：（1）由折叠可知：△ANM≌△ADM，∴∠MAN=∠DAM，∵AN平分∠MAB，∴∠MAN=∠NAB，∴∠DAM=∠MAN=∠NAB．∵四边形ABCD是矩形，∴∠DAB=90°，∴∠DAM=30°，∴DM=ADtan∠DAM=
=
；
（2）如图1，延长MN交AB延长线于点Q，∵四边形ABCD是矩形，∴AB∥DC，∴∠DMA=∠MAQ．由折叠可知：△ANM≌△ADM，∴∠DMA=∠AMQ，AN=AD=3，MN=MD=1，∴∠MAQ=∠AMQ，∴MQ=AQ．
设NQ=x，则AQ=MQ=1+x．在Rt△ANQ中， 
，∴
，解得：x=4．
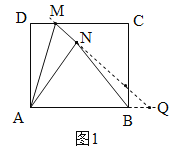
∴NQ=4，AQ=5，∵AB=4，AQ=5，∴
=
=
ANNQ=
；
（3）如图2，过点A作AH⊥BF于点H，则△ABH∽△BFC，∴
.∵AH≤AN=3，AB=4，∴当点N、H重合（即AH=AN）时，DF最大．（AH最大，BH最小，CF最小，DF最大）
此时M、F重合，B、N、M三点共线，△ABH≌△BFC（如图3），∴CF=BH=
=
=
，∴DF的最大值为：
．
