题目内容
如图，是12×12的正方形（每个小正方形边长均为1个单位）的网格．
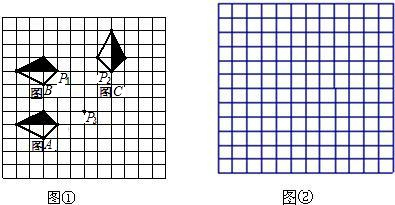
（1）在图①中建立适当的直角坐标系使点P1，P3的坐标分别为（-1，2）、（1，-1）．将图A通过平移或旋转这两种变换得到图C可用以下三种办法：
方法1：将图形A向______（填“上”或“下”）平移______个单位，得到图形B，再将图形B向右平移______个单位后，再绕点P2按顺时针方向旋转______得到图形C；
方法2：先将图形A平移到图形B，再将图形B绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是______；
方法3：直接将图形A绕某点R顺时针旋转______°得到图形C，则点R的坐标是______；
（2）在图②中画一个格点四边形EFGH，使它为轴对称图形且面积等于图A面积的3倍（除矩形外）．
解：（1）根据平移变换的性质可知：
方法1：将图形A向上平移4个单位，得到图形B，再将图形B向右平移4个单位后，再绕点P2按顺时针方向旋转90°得到图形C；
方法2：先将图形A平移到图形B，再将图形B绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是（1，0）；
方法3：直接将图形A绕某点R顺时针旋转90°得到图形C，则点R的坐标是（3，-2）；
（2）如图．
分析：（1）按要求作图，利用对应点的坐标及位置寻找平移及旋转方法；
（2）由图形可知，图A的面积=3，所以四边形EFGH的面积=9，据此设计图形即可．
点评：本题需仔细分析图形，利用对应点的坐标寻找变换规律，进而解决问题．
方法1：将图形A向上平移4个单位，得到图形B，再将图形B向右平移4个单位后，再绕点P2按顺时针方向旋转90°得到图形C；
方法2：先将图形A平移到图形B，再将图形B绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是（1，0）；
方法3：直接将图形A绕某点R顺时针旋转90°得到图形C，则点R的坐标是（3，-2）；
（2）如图．
分析：（1）按要求作图，利用对应点的坐标及位置寻找平移及旋转方法；
（2）由图形可知，图A的面积=3，所以四边形EFGH的面积=9，据此设计图形即可．
点评：本题需仔细分析图形，利用对应点的坐标寻找变换规律，进而解决问题．
练习册系列答案
相关题目
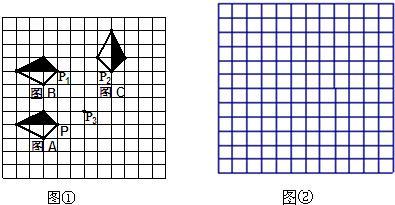23、如图，是12×12的正方形（每个小正方形边长均为1个单位）的网格．
（2012•利川市二模）学习完概率与统计知识后，小兵对本校同年级同学的年龄进行了随机抽样调查，如图，是他通过收集、整理后绘制的条形统计图．请根据图中提供的信息解答下列问题：