题目内容
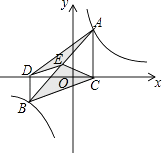
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 
【答案】![]()
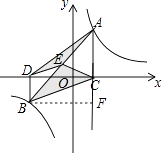
【解析】解:过点B作直线AC的垂线交直线AC于点F,如图所示. ∵△BCE的面积是△ADE的面积的2倍,E是AB的中点,
∴S△ABC=2S△BCE , S△ABD=2S△ADE ,
∴S△ABC=2S△ABD , 且△ABC和△ABD的高均为BF,
∴AC=2BD,
∴OD=2OC.
∵CD=k,
∴点A的坐标为( ![]() ,3),点B的坐标为(﹣
,3),点B的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴AC=3,BD= ![]() ,
,
∴AB=2AC=6,AF=AC+BD= ![]() ,
,
∴CD=k= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用比例系数k的几何意义对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 15 | 12 |
月污水处理能力(吨/月) | 250 | 200 |
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.