题目内容
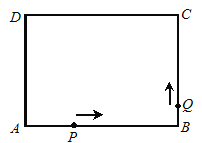
【题目】如图,矩形ABCD中,AB=4,BC=3,点P、Q分别从A、B两点出发,按逆时针方向沿矩形的边运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,运动的时间为t秒,当其中某一点到达点A时,运动停止,运动过程中,点P关于直线AQ的对称点记为点M.
(1)点P点在线段AB上运动,点Q在线段BC上运动时,请用含t的式子表示出△APQ的面积S;
(2)当点P在线段BC上运动,且△ABP∽△PCQ时,求t的值;
(3)若点Q在线段CD上,且以A、P、Q、M为顶点的四边形是菱形,求t的值.
【答案】(1)S=t2 (2)![]() (3)当t=1+
(3)当t=1+![]() 时,以A、P、Q、M为顶点的四边形是菱形
时,以A、P、Q、M为顶点的四边形是菱形
【解析】试题分析:(1)底AP=2t,高BQ=t,根据三角形性的的面积公式求解即可;
(2)根据相似三角形的性质列方程求解;
(3)分四种情况,①点P在BC上,点Q在CD上,此时不合题意;②点P和点Q都在CD上,P在Q的左边,此时不合题意;③点P和点Q都在CD上,P在Q的又边,根据勾股定理列方程求解;④点P在AD上,点Q在CD上,根据勾股定理列方程求解.
解:(1)AP=2t,BQ=t,∴S=t2.
(2)如图1,由△ABP∽△PCQ可知,此时点Q在线段CD上,∴![]() ,
,
即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() .
.
(3)①当3<t≤![]() 时,如图2,以A、P、Q、M为顶点的四边形不可能是菱形;
时,如图2,以A、P、Q、M为顶点的四边形不可能是菱形;
②当![]() <t≤4时,如图3,以A、P、Q、M为顶点的四边形不可能是菱形;
<t≤4时,如图3,以A、P、Q、M为顶点的四边形不可能是菱形;
③当4<t≤![]() 时,如图4,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即32+(11-2t)2=(2t-t-4)2,整理得t2-12t+38=0,方程无解;
时,如图4,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即32+(11-2t)2=(2t-t-4)2,整理得t2-12t+38=0,方程无解;
④当![]() <t≤7时,如图5,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即(2t-11)2+(7-t)2=(14-2t)2,解得t=1±
<t≤7时,如图5,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即(2t-11)2+(7-t)2=(14-2t)2,解得t=1±![]() ,
,
∵![]() <t≤7,∴t=1+
<t≤7,∴t=1+![]() .
.
∴当t=1+![]() 时,以A、P、Q、M为顶点的四边形是菱形.
时,以A、P、Q、M为顶点的四边形是菱形.



 53随堂测系列答案
53随堂测系列答案