题目内容
【题目】如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了 ![]() 秒。
秒。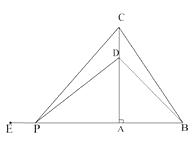
(1)求AD的长;
(2)直接写出用含有 ![]() 的代数式表示PE=;
的代数式表示PE=;
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出 ![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
【答案】
(1)解:∵∠BAC=90°,AB=6cm,BC=10cm,
∴AC= ![]() =8cm,
=8cm,
∵CD=2cm,
∴AD=6cm。
(2)2t
(3)解:存在;当△ABC≌△ADP时AP=AC=8cm
∴PE=10-8=2 cm
∴t=1
当△ABC≌△APD时AP=AB=6 cm
∴PE=10-6=4 cm
∴t=4
【解析】解:(2)因为动点P从BA延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒,所以PE=2t。在三角形BAC中用勾股定理可求AC的长,则AD=AC-CD;(2)用含有 t 的代数式表示PE=2t;(3)存在。理由略。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目