题目内容
【题目】如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证: 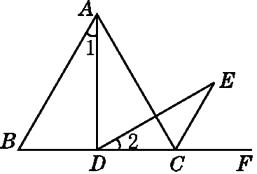
(1)∠1=∠2;
(2)AD=DE.
【答案】
(1)证明:∵△ABC是等边三角形,∠ADE=60°,
∴∠ADE=∠B=60°.
又∵∠ADC=∠2+∠ADE=∠1+∠B,∴∠1=∠2
(2)证明:如图,在AB上取一点M,使BM=BD,连接MD.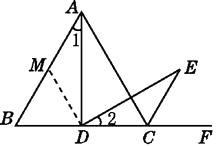
∵△ABC是等边三角形,
∴∠B=60°.
∴△BMD是等边三角形,
∴∠BMD=60°,
∴∠AMD=120°.
∵CE是∠ACF的平分线,
∴∠ECA=60°,
∴∠DCE=120°.
∴∠AMD=∠DCE=120°,
∵ AB=BC ,BM=BD,
∵BA-BM=BC-BD,
∴MA=CD.
在△AMD和△DCE中, 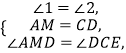
∴△AMD≌△DCE(ASA).
∴AD=DE 。
【解析】 (1)根据等边三角形的性质及已知得出∠ADE=∠B=60°,根据三角形的外角定理及角的和差得出∠ADC=∠2+∠ADE=∠1+∠B,从而得出∠1=∠2 ;
(2)根据等边三角形的性质得出∠B=60°,根据有一个角为60°的等腰三角形是等边三角形得出△BMD是等边三角形 ,等边三角形三个内角都是60°及邻补角的定义得出∠AMD=120°,根据角平分线的定义及角的和差得出∠DCE=120°,从而得出∠AMD=∠DCE=120°,根据等式的性质得出MA=CD,从而利用ASA判断出△AMD≌△DCE,利用全等三角形对应边相等得出AD=DE。

练习册系列答案
相关题目