Question

【题目】如图，∠AOB＝30°，点M，N分别在边OA，OB上，且OM＝1，ON＝3，点P，Q分别在边OB，OA上，求MP＋PQ＋QN的最小值．

Answer 1

【答案】

【解析】试题分析：如解图，作点M关于OB的对称点M1，作点N关于OA的对称点N1，连结M1N1分别交OA，OB于点Q，P，此时MP＋PQ＋QN的值最小．

试题解析：

如解图，作点M关于OB的对称点M1，作点N关于OA的对称点N1，连结M1N1分别交OA，OB于点Q，P，

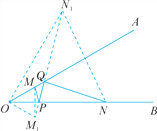
由对称的性质，知M1P＝MP，N1Q＝NQ，

∴MP＋PQ＋QN＝M1N1.

则∠M1OP＝∠POM＝∠N1OM＝30°，

∴∠N1OM1＝90°.

又∵ON1＝ON＝3，OM1＝OM＝1，

∴M1N1＝＝，即MP＋PQ＋QN的最小值为 .