题目内容
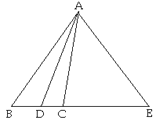
【题目】如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，并且AE＝
(AB＋AD)，求∠ABC＋∠ADC的度数．
【答案】180°
【解析】
延长AD过C作CF⊥AD于F，由条件可证△AFC≌△AEC，得到CF=CE．再由条件
可证BE=DF，所以△CDF≌△CEB，由全等的性质可得∠ABC=∠CDF，问题可得解．
过C作CF⊥AD于F．
∵AC平分∠BAD，∴∠FAC=∠EAC．
∵CE⊥AB，CF⊥AD，∴∠DFC=∠CEA=90°，∴△AFC≌△AEC（AAS），∴AF=AE，CF=CE．
∵，∴2AE=AB+AD．
又∵AD=AF﹣DF，AB=AE+BE，AF=AE，∴2AE=AE+BE+AE﹣DF，∴BE=DF．
∵∠DFC=∠CEB=90°，CF=CE，∴△CDF≌△CEB（SAS），∴∠ABC=∠CDF．
∵∠ADC+∠CDF=180°，∴∠ABC+∠ADC=180°．
练习册系列答案
相关题目
【题目】为了解饮料自动售货机的销售情况，有关部门从北京市所有的饮料自动售货机中随机抽取20台进行了抽样调查，记录下某一天各自的销售情况
单位：元
，并对销售金额进行分组，整理成如下统计表：
28，8，18，63，15，30，70，42，36，47，
25，58，64，58，55，41，58，65，72，30
销售金额x |
|
|
|
|
划记 |
|
| ______ | ______ |
频数 | 3 | 5 | ______ | ______ |
请将表格补充完整；
用频数分布直方图将20台自动售货机的销售情况表示出来，并在图中标明相应数据；
根据绘制的频数分布直方图，你能获取哪些信息？至少写出两条不同类型信息
