题目内容
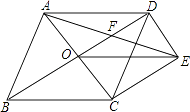
【题目】已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF. 求证:四边形BCFE是菱形.
【答案】解:∵BE=2DE,EF=BE, ∴EF=2DE.
∵D、E分别是AB、AC的中点,
∴BC=2DE且DE∥BC.
∴EF=BC.
又EF∥BC,
∴四边形BCFE是平行四边形.
又EF=BE,
∴四边形BCFE是菱形.
【解析】由题意易得,EF与BC平行且相等,∴四边形BCFE是平行四边形.又EF=BE,∴四边形BCFE是菱形.
【考点精析】利用菱形的判定方法对题目进行判断即可得到答案,需要熟知任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
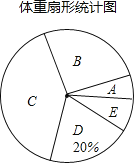
【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
体重频数分布表
组边 | 体重(千克) | 人数 |
A | 45≤x<50 | 12 |
B | 50≤x<55 | m |
C | 55≤x<60 | 80 |
D | 60≤x<65 | 40 |
E | 65≤x<70 | 16 |
(1)填空:①m=__(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于__度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?