题目内容
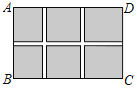
【题目】如图，某小区计划在一个长 80米，宽 36米的长方形场地 ABCD上，修建三条同样宽的道路，使其中两条与 AB平行，另一条与 AD平行，其余部分种草，若使每块草坪的面积 都为 260平方米，求道路的宽度．设道路宽度为 x米，则根据题意可列方程为（ ）
A.（80－2x）（36－x）=260×6B.36×80－2×36x－80x=260×6
C.（36－2x）（80－x）=260D.（80－2x）（36－x）=260
【答案】A
【解析】
设道路的宽度为x米．则横、纵道路的宽分别为x米、2x米，则草坪的总面积是相邻两边的长度分别为（80-2x）米、（36-x）米的矩形面积，根据每一块草坪的面积都为260平方米，即可得出关于x的一元二次方程，即可得出结论．
解：设道路的宽度为x米，则横、纵道路的宽分别为x米、2x米，则草坪的总面积是相邻两边的长度分别为（80-2x）米、（36-x）米的矩形面积，
根据题意得：（80-2x）（36-x）=260×6，
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
