题目内容
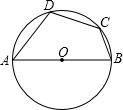
如图,⊙O半径为2,直径CD以O为中心,在⊙O所在平面内转动,当CD转动时,OA固定不动,0°≤∠DOA≤90°,且总有BC∥OA,AB∥CD,若OA=4,BC与⊙O交于E,连AD,设CE为x,四边形ABCD的面积为y.
(1)求y关于x的函数解析式,并指出x的取值范围;
(2)当x=2
时,求四边形ABCD在圆内的面积与四边形ABCD的面积之比;
(3)当x取何值时,四边形ABCD为直角梯形?连EF,此时OCEF变成什么图形?(只需说明结论,不必证明)

(1)求y关于x的函数解析式,并指出x的取值范围;
(2)当x=2
| 3 |
(3)当x取何值时,四边形ABCD为直角梯形?连EF,此时OCEF变成什么图形?(只需说明结论,不必证明)

(1)连接DE,过O作OH⊥BC于H,则DE⊥BC,OH∥DE,
∵CD=4,CE=x,
∴DE=
=
=
,
∴OH=
DE=
,
∴y=S?ABCO+S△OAD=4×
+
×4×
,
=3
(0≤x≤4),
∴x的取值范围为0≤x≤4;
(2)当x=2
时,
∵CE=2
,CD=4,
∴DE=2,∠C=30°,
∴∠DOE=60°,OH=1,
∵S圆内部分=
+
×2
×1=
+
,
∵S四边形ABCD=3
=3
=6,
∴S圆内部分:S四边形ABCD=
,
∴四边形ABCD在圆内的面积与四边形ABCD的面积之比为(2π+3
):18;
(3)当∠CDA=90°,
由OA=2OD,得∠DAO=30°
所以∠DCB=∠DOA=60°
此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
连EF,此时OCEF变成了菱形

∵CD=4,CE=x,
∴DE=
| CD2-CE2 |
| 42-x2 |
| 16-x2 |
∴OH=
| 1 |
| 2 |
| ||
| 2 |
∴y=S?ABCO+S△OAD=4×
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=3
| 16-x2 |
∴x的取值范围为0≤x≤4;
(2)当x=2
| 3 |
∵CE=2
| 3 |
∴DE=2,∠C=30°,
∴∠DOE=60°,OH=1,
∵S圆内部分=
| 60×π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
| 3 |
∵S四边形ABCD=3
| 16-x2 |
| 16-12 |
∴S圆内部分:S四边形ABCD=
2π+3
| ||
| 18 |
∴四边形ABCD在圆内的面积与四边形ABCD的面积之比为(2π+3
| 3 |
(3)当∠CDA=90°,
由OA=2OD,得∠DAO=30°
所以∠DCB=∠DOA=60°
此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
连EF,此时OCEF变成了菱形


练习册系列答案
相关题目



 长线交⊙O于N,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,NE的延长线交⊙O于M.
长线交⊙O于N,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,NE的延长线交⊙O于M.