题目内容
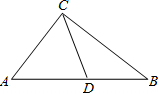
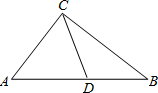 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=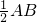 .(此定理在解决下面的问题中要用到)
.(此定理在解决下面的问题中要用到)
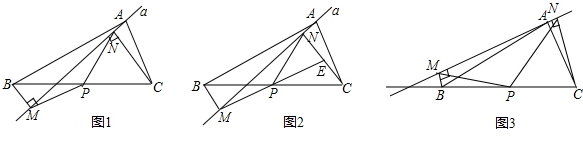
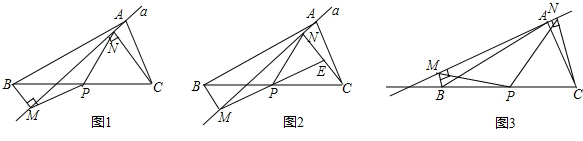
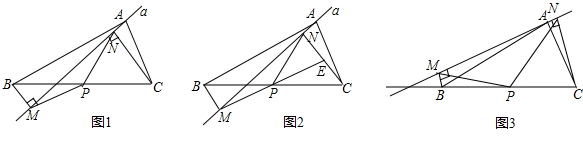
应用:如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;
(1)延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明:若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
(1)①证明:∵BM⊥直线a,CN⊥直线a,
∴∠BMN=∠CNM=90°,
∴BM∥CN,
∴∠MBP=∠PCE,
∵点P为BC边中点,
∴BP=PC,
在△BPM和△CPE中,
 ,
,
∴△BPM≌△CPE(ASA);
②∵△BPM≌△CPE,
∴MP=PE,
∵∠MNE=90°,
∴PN=PM;
(2)PM=PN还成立.
理由如下:如图3,延长MP与NC延长线交于F,
 ∵BM⊥直线a,CN⊥直线a,
∵BM⊥直线a,CN⊥直线a,
∴BM∥FN,
∴∠BMP=∠PFC,
∵点P为BC边中点,
∴BP=PC,
在△BMP和△CFP中,
 ,
,
∴△BMP≌△CFP(ASA),
∴PM=PF,
∵∠MNF=90°,
∴PM=PN;
(3)四边形MBCN是矩形,PM=PN还成立.
理由如下:如图4,∵a∥BC,BM⊥a,CN⊥a,
∴BM∥CN,BM=CN,
∴四边形MBCN是矩形,
∵点P是BC的中点,
∴BP=CP,
在△BMP和△CMN中,
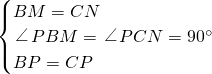 ,
,
∴△BMP≌△CPN(SAS),
∴PM=PN.
分析:(1)①根据垂直的定义以及平行线的判定可得BM∥CN,再根据两直线平行,内错角相等可得∠MBP=∠PCE,然后利用“角边角”证明即可;②根据全等三角形对应边相等可得MP=PE,在Rt△MNE中,利用直角三角形斜边上的中线等于斜边的一半解答;
(2)延长MP与NC延长线交于F,然后与(1)同理可证;
(3)根据矩形的判定解答,再利用“边角边”证明△BMP和△CPN全等,根据全等三角形对应边相等即可得证.
点评:本题考查了旋转的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,矩形的判定,读懂题目信息并灵活运用,作辅助线构造出全等三角形是解题的关键.
∴∠BMN=∠CNM=90°,
∴BM∥CN,
∴∠MBP=∠PCE,
∵点P为BC边中点,
∴BP=PC,
在△BPM和△CPE中,
 ,
,∴△BPM≌△CPE(ASA);
②∵△BPM≌△CPE,
∴MP=PE,
∵∠MNE=90°,
∴PN=PM;
(2)PM=PN还成立.
理由如下:如图3,延长MP与NC延长线交于F,
 ∵BM⊥直线a,CN⊥直线a,
∵BM⊥直线a,CN⊥直线a,∴BM∥FN,
∴∠BMP=∠PFC,
∵点P为BC边中点,
∴BP=PC,
在△BMP和△CFP中,
 ,
,∴△BMP≌△CFP(ASA),
∴PM=PF,
∵∠MNF=90°,
∴PM=PN;
(3)四边形MBCN是矩形,PM=PN还成立.
理由如下:如图4,∵a∥BC,BM⊥a,CN⊥a,
∴BM∥CN,BM=CN,
∴四边形MBCN是矩形,
∵点P是BC的中点,
∴BP=CP,
在△BMP和△CMN中,
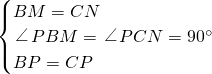 ,
,∴△BMP≌△CPN(SAS),
∴PM=PN.
分析:(1)①根据垂直的定义以及平行线的判定可得BM∥CN,再根据两直线平行,内错角相等可得∠MBP=∠PCE,然后利用“角边角”证明即可;②根据全等三角形对应边相等可得MP=PE,在Rt△MNE中,利用直角三角形斜边上的中线等于斜边的一半解答;
(2)延长MP与NC延长线交于F,然后与(1)同理可证;
(3)根据矩形的判定解答,再利用“边角边”证明△BMP和△CPN全等,根据全等三角形对应边相等即可得证.
点评:本题考查了旋转的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,矩形的判定,读懂题目信息并灵活运用,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
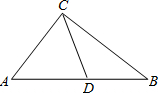 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=