题目内容
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点
向终点![]() 运动;动点
运动;动点![]() 从点
从点![]() 同时出发,以每秒1个单位长度的速度沿边
同时出发,以每秒1个单位长度的速度沿边![]() 向终点
向终点![]() 运动,设运动的时间为
运动,设运动的时间为![]() 秒,
秒,![]() .
.
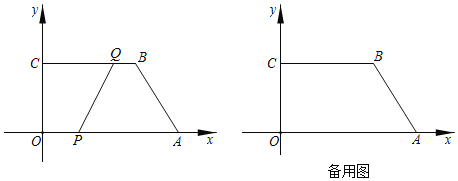
(1)直接写出![]() 关于
关于![]() 的函数解析式及
的函数解析式及![]() 的取值范围:_______;
的取值范围:_______;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)连接![]() 交
交![]() 于点
于点![]() ,若双曲线
,若双曲线![]() 经过点
经过点![]() ,问
,问![]() 的值是否变化?若不变化,请求出
的值是否变化?若不变化,请求出![]() 的值;若变化,请说明理由.
的值;若变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)经过点
;(3)经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值不变.
值不变.![]() 值为
值为![]() .
.
【解析】
(1)过点P作PE⊥BC于点E,依题意求得P、Q的坐标,进而求得PE、EQ的长,再利用勾股定理即可求得答案,由时间=距离![]() 速度可求得t的取值范围;
速度可求得t的取值范围;
(2)当![]() ,即
,即![]() 时,代入(1)求得的函数中,解方程即可求得答案;
时,代入(1)求得的函数中,解方程即可求得答案;
(3)过点![]() 作
作![]() 于点
于点![]() ,求得OB的长,由
,求得OB的长,由![]() ,可求得
,可求得![]() ,继而求得OD的长,利用三角函数即可求得点D的坐标,利用反比例函数图象上点的特征即可求得
,继而求得OD的长,利用三角函数即可求得点D的坐标,利用反比例函数图象上点的特征即可求得![]() 值.
值.
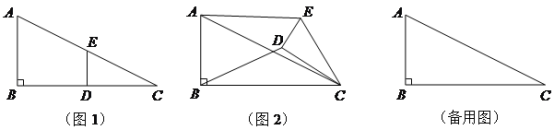
(1)过点P作PE⊥BC于点E,如图1:
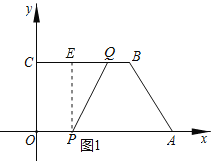
∵点B、C纵坐标相同,
∴BC⊥y轴,
∴四边形OPEC为矩形,
∵运动的时间为![]() 秒,
秒,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
点Q运动的时间最多为:![]() (秒) ,
(秒) ,
点P运动的时间最多为:![]() (秒) ,
(秒) ,
∴![]() 关于
关于![]() 的函数解析式及
的函数解析式及![]() 的取值范围为:
的取值范围为:![]() ;
;
(2)当![]() 时,
时,![]()
整理,得![]() ,
,
解得:![]() ,
,![]() .
.
(3)经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值不变.
值不变.
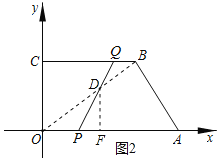
连接![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如下图2所示.
,如下图2所示.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴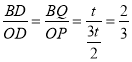 ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值为
值为![]() .
.

练习册系列答案
相关题目