Question

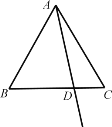
【题目】如图，的对角线，交于点，平分交于点，交于点，且，，连接.下列结论：①；②；③；④.其中正确的是（ ）

A.①②④B.①③④C.②③④D.①③

Answer 1

【答案】B

【解析】

根据三角形一边上的中线等于这边的一半则这个三角形是直角三角形对①进行判断；根据同高不等底的两个三角形面积的比是底的比对②进行判断；利用勾股定理及直角三角形中的角的性质进行计算求得对③进行判断；根据平行线分线段成比例定理并利用中间比对④进行判断.

∵四边形ABCD是平行四边形，
∴∠ABC=∠ADC=60°，∠BAD=∠BCD =120°，
∵CE平分∠BCD交AB于点E，
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形，
∴BE=BC=CE，
∵AB=2BC，
∴AE=BC=CE，
∴∠ACB=90°，

∵四边形ABCD是平行四边形，

∴，又∵AE= BE

∴OE是的中位线，

∴OE∥BC，

∴EO⊥AC，故①正确；

∵OE是的中位线，

∴OE∥BC，BC=2OE，

∴，

∴，

∴，

∵由和同高不等底，

∴，

∴，故②错误；

在中，∠ACB=90°，∠CAB=30°，

设，则

∴

∴

在中，∠OCB=90°，

∴

∴

∴，故③正确；

∵OE∥BC，

∴，

∵BE∥DC，

∴，

∴，

∴，故④正确；

综上：①③④正确，

故选：B