题目内容
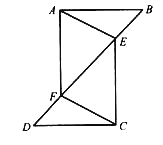
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
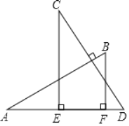
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
【答案】D
【解析】
根据垂直和平行线性质,证明角相等,证明△ABF≌△CDE(AAS),得到AF=CE=a,BF=DE=b,可得AD=AF+DE-EF=a+b-c.
如图,记AB与CD的交点为G,BF与CD的交点为H,

∵CE⊥AD,
BF⊥AD,
∴CE∥BF,
∴∠C=∠BHG,
∵AB⊥CD,
∴∠BGH=∠BFA=90,
∠B=∠B,
∴∠BHG=∠A,
∴∠A=∠C,
∠AFB=∠CED=90,
AB=CD,
∴△ABF≌△CDE(AAS),
∴AF=CE=a,
BF=DE=b,
∴AD=AF+DE-EF=a+b-c.
故选:D

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目