题目内容
如图,已知二次函数y=x2-2x-1的图象的顶点为A,二次函数y=ax2+bx+c的图象与x轴交于原点O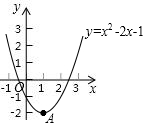 及另一点C.它的顶点B在函数y=x2-2x-1的图象的对称轴上.
及另一点C.它的顶点B在函数y=x2-2x-1的图象的对称轴上.(1)求点A与点C的坐标;
(2)当点B与点A关于x轴对称时,求函数y=ax2+bx+c的解析式,并判断这个四边形AOBC能否通过一个直径为1.8的圆孔.
分析:(1)将二次函数y=x2-2x-1化为顶点式,就可以求出顶点A的坐标,利用抛物线的对称性就可以求出OF=CF,从而求出C的坐标.
(2)通过第一问可以求出A、O、B、C的坐标,从而可以求得四边形AOBC是菱形,而短的对角线长为2>1.8,从判断可以通过一个直径为1.8的圆孔.
(2)通过第一问可以求出A、O、B、C的坐标,从而可以求得四边形AOBC是菱形,而短的对角线长为2>1.8,从判断可以通过一个直径为1.8的圆孔.
解答: 解:(1)∵y=x2-2x-1,
解:(1)∵y=x2-2x-1,
∴y=(x-1)2-2,
∴A(1,-2),
∵y=ax2+bx+c的顶点B在函数y=x2-2x-1的图象的对称轴上,
如图得:∴OF=1根据抛物线的对称性得,
FC=1,
∴CO=2,
∴C(2,0);
(2)∵点B与点A关于x轴对称
∴B(1,2),
∴
,解得
,
∴抛物线的解析式为:y=-2x2+4x,
∵OC⊥AB,OF=CF,BF=AF,
∴四边形AOBC是菱形,
∵CO=2>1.8,
∴这个四边形AOBC能通过一个直径为1.8的圆孔.
 解:(1)∵y=x2-2x-1,
解:(1)∵y=x2-2x-1,∴y=(x-1)2-2,
∴A(1,-2),
∵y=ax2+bx+c的顶点B在函数y=x2-2x-1的图象的对称轴上,
如图得:∴OF=1根据抛物线的对称性得,
FC=1,
∴CO=2,
∴C(2,0);
(2)∵点B与点A关于x轴对称
∴B(1,2),
∴
|
|
∴抛物线的解析式为:y=-2x2+4x,
∵OC⊥AB,OF=CF,BF=AF,
∴四边形AOBC是菱形,
∵CO=2>1.8,
∴这个四边形AOBC能通过一个直径为1.8的圆孔.
点评:本题是一道二次函数的综合试题,考查了抛物线的顶点式,抛物线图象的对称性,待定系数法求函数的解析式等知识点.

练习册系列答案
相关题目
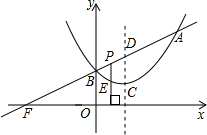 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.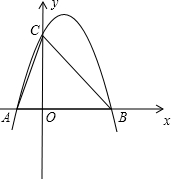
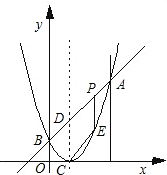 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.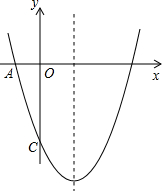 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).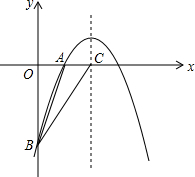 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数