题目内容
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.
![]()
【答案】7 2或4 1 ﹣2.5或4.5.
【解析】
(1)先求出![]() 的结果,再求出它的绝对值即可;
的结果,再求出它的绝对值即可;
(2)根据绝对值的性质得到![]() ,解方程即可求解;
,解方程即可求解;
(3)根据绝对值的意义,可知![]() 是数轴上表示数x的点与表示数3的点之间的距离,
是数轴上表示数x的点与表示数3的点之间的距离,![]() 是数轴上表示数x的点与表示数﹣1的点之间的距离,若
是数轴上表示数x的点与表示数﹣1的点之间的距离,若![]() ,则此点必在
,则此点必在![]() 与
与![]() 之间,故
之间,故![]() ,
,![]() ,由此可得到关于x的方程,求出x的值即可;
,由此可得到关于x的方程,求出x的值即可;
(4)由于![]() 及
及![]() 的符号不能确定,故应分
的符号不能确定,故应分![]() ,
,![]() ,
,![]() 三种情况解答.
三种情况解答.
解:(1)![]() 的值为7;
的值为7;
(2)∵![]() ,
,
∴![]() ,
,
解得x=2或4.
故x的值为2或4;
(3)根据绝对值的意义可知,此点必在![]() 与3之间,故
与3之间,故![]() ,
,![]() ,
,
∴原式可化为![]() ,
,
∴x=1.
故x的值为1;
(4)在数轴上3和![]() 的距离为4,则满足方程的x的对应点在
的距离为4,则满足方程的x的对应点在![]() 的左边或3的右边.
的左边或3的右边.
若x的对应点在![]() 的左边,则
的左边,则![]() ;
;
若x的对应点在3的右边,则![]() .
.
所以原方程的解是![]() 或x=4.5.
或x=4.5.
故x的值为![]() 或4.5.
或4.5.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
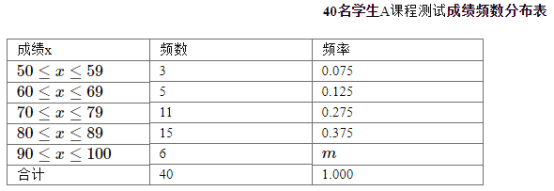
小学生10分钟应用题系列答案【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将![]() 地的茶叶1000吨和
地的茶叶1000吨和![]() 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的![]() 地和
地和![]() 地,
地,![]() 地和
地和![]() 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从![]() 、
、![]() 两地运茶叶到
两地运茶叶到![]() 、
、![]() 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设![]() 地运到
地运到![]() 地的茶叶为
地的茶叶为![]() 吨,
吨,
|
| |
| 35 | 40 |
| 30 | 45 |
(1)用含![]() 的代数式填空:
的代数式填空:![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________.
地的茶叶吨数为___________.
(2)用含![]() (吨)的代数式表示总运费
(吨)的代数式表示总运费![]() (元),并直接写出自变量
(元),并直接写出自变量![]() 的取值范围;
的取值范围;
(3)求最低总运费,并说明总运费最低时的运送方案.