题目内容
【题目】
如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如图①:求证∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数

【答案】(1)证明见解析;(2)60°;(3)∠EFB=30°或120°.
【解析】
试题分析:(1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用等腰三角形的性质结合垂直的定义得出∠DAB的度数;
(3)利用正方形的性质结合等腰三角形的性质得出①当F在AB延长线上时,以及②当F在线段AB上时,分别求出即可.
试题解析:(1)∵四边形ABCD为菱形,
∴DC=CB,
在△DCE和△BCE中,
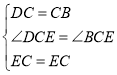 ,
,
∴△DCE≌△BCE(SAS),
∴∠EDC=∠EBC,
∵DC∥AB,
∴∠EDC=∠AFD,
∴∠AFD=∠EBC;
(2)∵DE=EC,
∴∠EDC=∠ECD,
设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°,
由BE⊥AF得:2x+x=90°,
解得:x=30°,
∴∠DAB=∠CBF=60°;
(3)分两种情况:
①如图1,当F在AB延长线上时,
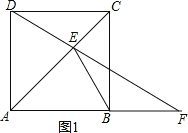
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:
90+x+x+x=180,
解得:x=30,
∴∠EFB=30°;
②如图2,当F在线段AB上时,
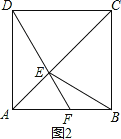
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°,
综上:∠EFB=30°或120°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目