题目内容
【题目】小龙在学校组织的社会调查活动中负贵了解他所居住的小区450户居民的家庭收入情况从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频分布直方图。
分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1400≤ | ||
1600≤ | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题
(1)补全频数分布表
(2)补全频数分布直方图
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户
【答案】(1)18，1200≤
＜1400，3，7.5%，5%；(2)见解析；(3) 338
【解析】
（1）根据1000≤＜1200所占的百分比，计算1000≤＜1200频数即可；再根据总数即可计算出1400≤＜1600的频数，进而计算百分比.
（2）根据频数表补充分布直方图即可.
（3）首先计算出大于1000不足1600元所占的百分比，再根据总数计算即可.
解：
(1)4
，
根据直方图可得1200≤＜1400，
，
，
(2)根据频数表补充如下：
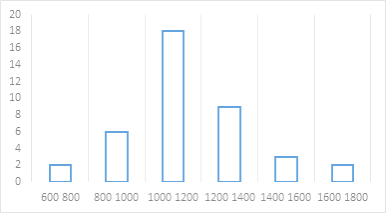
(3)450×75%=338
估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有338户
【题目】在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案，也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留一丝空隙，又不互相重叠(在数学上叫做平面镶嵌)．这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时，就拼成了一个平面图形．
(1)请你根据图中的图形，填写表中空格：
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
正多边形每个内角度数 | 60° | 90° | 108° | 120° | …… |
(2)如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？
