题目内容
【题目】已知抛物线的解析式为
.
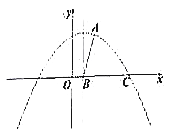
（1）当自变量
时，函数值
随
的增大而减少，求
的取值范围；
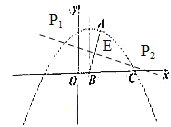
（2）如图，若抛物线的图象经过点
，与
轴交于点
，抛物线的对称轴与
轴交于
.
①求抛物线的解析式；
②在抛物线上是否存在点
，使得
？若存在，求出点
的坐标；若不存在，请说明理由.
【答案】(1)b≥0;(2)①
；②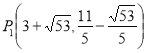
,
.
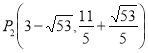【解析】
试题分析：(1)当自变量
时，函数值
随
的增大而减少,可得
,所以b≥0；（2）①把
代入
，得
；②作线段AB的垂直平分线，交抛物线于两点，此时
.
试题解析：
（1）∵自变量时，函数值随的增大而减少
∴对称轴在直线x=2的右边
∴
b≥0
(2)①把代入，得
∴
②存在
作线段AB的垂直平分线，与抛物线交于两点，此时
抛物线的对称轴是直线x=1，则B（1，0）
∵
∴直线AB表达式y=5x-5，E(1.5,2.5)
∴直线
表达式k=
设直线
表达式
把E(1.5,2.5)代入表达式得，b=2.8
直线表达式
由题意得
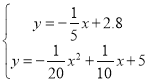
解得
，
∴,
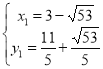
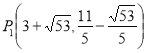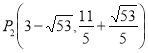
练习册系列答案
相关题目
【题目】在学校开展的“争做最优秀中学生”的一次演讲比赛中，编号1，2，3，4，5的五位同学最后成绩如表所示：那么这五位同学演讲成绩的众数与中位数依次是（ ）
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A.96，88
B.86，88
C.88，86
D.86，86
