题目内容
（2006•菏泽）（非课改区）如图：PT是⊙O的切线，T为切点，PB是⊙O的割线交⊙O于A，B两点，交弦CD于点M，已知CM=10，MD=2，PA=MB=4，则PT的长等于 ．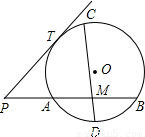
【答案】分析：由相交弦定理得AM•MB=CM•MD，由此求出AM=5，再由切割线定理得PT2=PA•PB即可求出PT．
解答：解：由相交弦定理得，AM•MB=CM•MD，
而CM=10，MD=2，PA=MB=4，
∴AM=5；
由切割线定理得，
PT2=PA•PB
=4×（4+5+4）
=4×13，
∴PT=2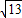
．
故填空答案：2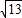
．
点评：本题主要利用了相交弦定理，切割线定理求解；解题时相关结论的字母容易出现错误，要仔细解答．
解答：解：由相交弦定理得，AM•MB=CM•MD，
而CM=10，MD=2，PA=MB=4，
∴AM=5；
由切割线定理得，
PT2=PA•PB
=4×（4+5+4）
=4×13，
∴PT=2
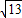．故填空答案：2
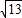．点评：本题主要利用了相交弦定理，切割线定理求解；解题时相关结论的字母容易出现错误，要仔细解答．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
