题目内容
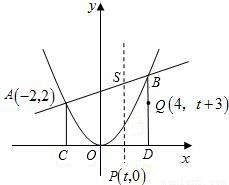
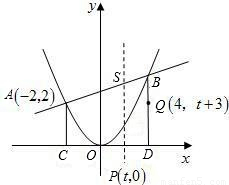
(2006•菏泽)如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(-2,2),B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),Q(4,t+3)分别为线段CD和BD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)指出二次函数中,函数y随自变量x增大或减小的情况;
(3)当SR=2RP时,求t的值;
(4)当S△BRQ=15时,求t的值.
【答案】分析:(1)将A点的坐标分别代入直线和抛物线中,即可求得两函数的解析式,然后联立两函数可求出B点坐标;
(2)可根据抛物线的对称轴和开口方向进行判断;
(3)可分别求出当x=t时,S,R的纵坐标,RP为R的纵坐标,SR为S,R的纵坐标差的绝对值,据此可求出t的值.(也可理解为SR为当x=t时,两函数的函数值的差,据此可列出关于t的方程,可求出t的值);
(4)本题可先求出BQ的长,然后根据R、B的横坐标求出△BRQ底边BQ上的高,由此可得出关于三角形BRQ的面积与t的函数关系式,将S=15代入函数式中即可求出t的值.
解答:解:(1)由题意知点A(-2,2)在y=ax2的图象上,又在y=x+b的图象上所以得
2=a(-2)2和2=-2+b,
∴a= ,b=4.
,b=4.
∴一次函数的解析式为y=x+4.
二次函数的解析式为y= x2.
x2.
由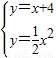 ,
,
解得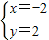 或
或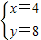 ,
,
所以B点的坐标为(4,8).
(2)对二次函数y= x2:
x2:
当x<0时,y随自变量x的增大而减小;
当x>0时,y随自变量x的增大而增大.
(3)因过点P(t,0)且平行于y轴的直线为x=t,
由 得
得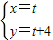 ,
,
所以点S的坐标(t,t+4).
由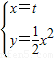 得
得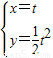 ,
,
所以点R的坐标(t, t2).
t2).
所以SR=t+4- t2,RP=
t2,RP= t2.
t2.
由SR=2RP得t+4- t2=2×
t2=2× t2,
t2,
解得t=- 或t=2.
或t=2.
因点P(t,0)为线段CD上的动点,
所以-2≤t≤4,
所以t=- 或t=2.
或t=2.
(4)因BQ=8-(t+3)=5-t,点R到直线BD的距离为4-t,
所以S△BPQ= (5-t)(4-t)=15.
(5-t)(4-t)=15.
解得t=-1或t=10.
因为-2≤t≤4,
所以t=-1.
点评:本题着重考查了待定系数法求二次函数解析式、图形面积的求法、函数图象交点等重要知识点.综合性强,考查学生数形结合的数学思想方法.
(2)可根据抛物线的对称轴和开口方向进行判断;
(3)可分别求出当x=t时,S,R的纵坐标,RP为R的纵坐标,SR为S,R的纵坐标差的绝对值,据此可求出t的值.(也可理解为SR为当x=t时,两函数的函数值的差,据此可列出关于t的方程,可求出t的值);
(4)本题可先求出BQ的长,然后根据R、B的横坐标求出△BRQ底边BQ上的高,由此可得出关于三角形BRQ的面积与t的函数关系式,将S=15代入函数式中即可求出t的值.
解答:解:(1)由题意知点A(-2,2)在y=ax2的图象上,又在y=x+b的图象上所以得
2=a(-2)2和2=-2+b,
∴a=
 ,b=4.
,b=4.∴一次函数的解析式为y=x+4.
二次函数的解析式为y=
 x2.
x2.由
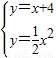 ,
,解得
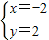 或
或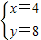 ,
,所以B点的坐标为(4,8).
(2)对二次函数y=
 x2:
x2:当x<0时,y随自变量x的增大而减小;
当x>0时,y随自变量x的增大而增大.
(3)因过点P(t,0)且平行于y轴的直线为x=t,
由
 得
得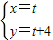 ,
,所以点S的坐标(t,t+4).
由
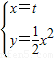 得
得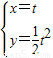 ,
,所以点R的坐标(t,
 t2).
t2).所以SR=t+4-
 t2,RP=
t2,RP= t2.
t2.由SR=2RP得t+4-
 t2=2×
t2=2× t2,
t2,解得t=-
 或t=2.
或t=2.因点P(t,0)为线段CD上的动点,
所以-2≤t≤4,
所以t=-
 或t=2.
或t=2.(4)因BQ=8-(t+3)=5-t,点R到直线BD的距离为4-t,
所以S△BPQ=
 (5-t)(4-t)=15.
(5-t)(4-t)=15.解得t=-1或t=10.
因为-2≤t≤4,
所以t=-1.
点评:本题着重考查了待定系数法求二次函数解析式、图形面积的求法、函数图象交点等重要知识点.综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目

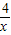 的图象与直线y=-
的图象与直线y=- x的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
x的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )