题目内容
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.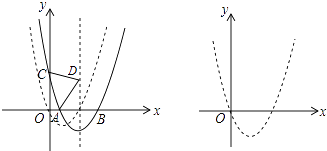
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
【答案】
(1)解:∵抛物线C1经过原点,与X轴的另一个交点为(2,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线C1的解析式为y=x2﹣2x,
∴抛物线C1的顶点坐标(1,﹣1).
(2)解:如图1,
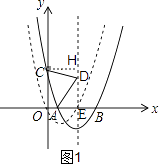
∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,
∴C2的解析式为y=(x﹣m﹣1)2﹣1,
∴A(m,0),B(m+2,0),C(0,m2+2m),
过点C作CH⊥对称轴DE,垂足为H,
∵△ACD为等腰直角三角形,
∴AD=CD,∠ADC=90°,
∴∠CDH+∠ADE=90°
∴∠HCD=∠ADE,
∵∠DEA=90°,
∴△CHD≌△DEA,
∴AE=HD=1,CH=DE=m+1,
∴EH=HD+DE=1+m+1=m+2,
由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),
∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)解:如图2,连接BC,BP,
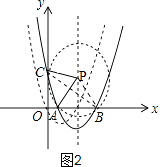
由抛物线对称性可知AP=BP,
∵△PAC为等边三角形,
∴AP=BP=CP,∠APC=60°,
∴C,A,B三点在以点P为圆心,PA为半径的圆上,
∴∠CBO= ![]() ∠CPA=30°,
∠CPA=30°,
∴BC=2OC,
∴由勾股定理得OB= ![]() =
= ![]() OC,
OC,
∴ ![]() (m2+2m)=m+2,
(m2+2m)=m+2,
解得m1= ![]() ,m2=﹣2(舍去),∴m=
,m2=﹣2(舍去),∴m= ![]() .
.
【解析】(1)把(0,0)及(2,,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标.
(2)先求出C2的解析式,确定A、B、C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△ACD为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值即可得出抛物线C2的解析式.
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=![]() OC,列出方程求出m的值即可.
OC,列出方程求出m的值即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 名校课堂系列答案
名校课堂系列答案【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?