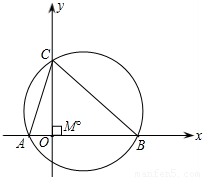题目内容
(2001•哈尔滨)已知:如图,梯形ABCD中,AD∥BC,AD=AB, ,梯形的高
,梯形的高 ,且
,且 .
.(1)求∠B的度数;
(2)设点M是梯形对角线AC上一点,DM的延长线与BC相交于点F,当
 时,求作以CF、DF的长为根的一元二次方程.
时,求作以CF、DF的长为根的一元二次方程.
【答案】分析:(1)本题可先表示出梯形ABCD的面积以及三角形ABC的面积,然后根据它们的比例关系可得出AD,BC的和与AD,BC的积的比例关系,然后将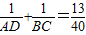 化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数.
化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数.
(2)本题的关键是求出CF,DF的长,题中给出了三角形ADM的面积,那么我们可通过作高线来求解.过M作两底的垂线交AD于H,交BC于N.那么根据三角形ADM的面积我们可求出MH的长,也就能求出MN的长,根据三角形ADM和FMC相似,我们可得出AD与FC的比应该等于两三角形的对应的高的比.这样就能求出CF的长,然后通过CF的长,判定出四边形ADFB是菱形,然后即可得出DF的长,这样就能求出所求的方程了.
解答:解:(1)∵S梯形ABCD= (AD+BC)•AE,S△ABC=
(AD+BC)•AE,S△ABC= BC•AE
BC•AE
∴ =
=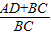 =
=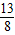 …①
…①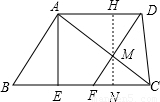
∵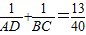
∴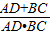 =
=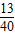 …②
…②
①÷②得:AD=5
∴AB=AD=5,BC=8
直角三角形ABE中,sinB=AB:AE=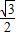
∴∠B=60°;
(2)过M作HN垂直于梯形ABCD的两底,且交AD于H,交BC于N.
S△ADM= AD•MH=
AD•MH= ×5•MH=
×5•MH=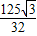
∴MH=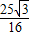
∴MN=AE-MH=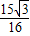
∵AD∥BC
∴△ADM∽△FCM
∴AD:FC=MH:MN,即5:FC=5:3
∴CF=3
∴BF=BC-CF=8-3=5=AD
∵AD∥BC
∴四边形ABFD是平行四边形
∵AD=AB=BF
∴四边形ABFD是菱形
∴DF=5
那么以CF,DF为根的一元二次方程就应该是x2-8x+15=0.
点评:本题主要考查了梯形的性质,相似三角形的判定和性质以及一元二次方程根与系数的关系等知识点,(2)中,通过作高和相似三角形来得出CF,DF的长是解题的关键.
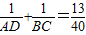 化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数.
化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数.(2)本题的关键是求出CF,DF的长,题中给出了三角形ADM的面积,那么我们可通过作高线来求解.过M作两底的垂线交AD于H,交BC于N.那么根据三角形ADM的面积我们可求出MH的长,也就能求出MN的长,根据三角形ADM和FMC相似,我们可得出AD与FC的比应该等于两三角形的对应的高的比.这样就能求出CF的长,然后通过CF的长,判定出四边形ADFB是菱形,然后即可得出DF的长,这样就能求出所求的方程了.
解答:解:(1)∵S梯形ABCD=
 (AD+BC)•AE,S△ABC=
(AD+BC)•AE,S△ABC= BC•AE
BC•AE∴
 =
=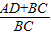 =
=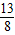 …①
…①
∵
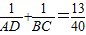
∴
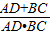 =
=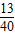 …②
…②①÷②得:AD=5
∴AB=AD=5,BC=8
直角三角形ABE中,sinB=AB:AE=
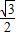
∴∠B=60°;
(2)过M作HN垂直于梯形ABCD的两底,且交AD于H,交BC于N.
S△ADM=
 AD•MH=
AD•MH= ×5•MH=
×5•MH=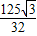
∴MH=
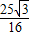
∴MN=AE-MH=
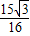
∵AD∥BC
∴△ADM∽△FCM
∴AD:FC=MH:MN,即5:FC=5:3
∴CF=3
∴BF=BC-CF=8-3=5=AD
∵AD∥BC
∴四边形ABFD是平行四边形
∵AD=AB=BF
∴四边形ABFD是菱形
∴DF=5
那么以CF,DF为根的一元二次方程就应该是x2-8x+15=0.
点评:本题主要考查了梯形的性质,相似三角形的判定和性质以及一元二次方程根与系数的关系等知识点,(2)中,通过作高和相似三角形来得出CF,DF的长是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目