题目内容
(2001•哈尔滨)已知:如图,抛物线y=ax2+bx+c与x轴交于A、B两点,它们的横坐标分别为-1和3,与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.(1)求这条抛物线的解析式;
(2)求图象经过M、A两点的一次函数解析式;
(3)在(1)中的抛物线上是否存在点P,使过P、M两点的直线与△ABC的两边AB、BC的交点E、F和点B所组成的△BEF和△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
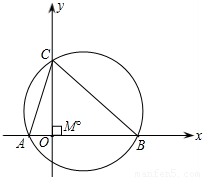
【答案】分析:(1)根据题意即可得出A、B、C三点的坐标,可通过待定系数法求出抛物线的解析式.
(2)本题的关键是求出M点的坐标,可如果设圆M与y轴的另一交点为D,那么可根据相交弦定理求出OD的长,进而可求出M点的纵坐标,同理可求出M的横坐标,得出M的坐标后可用待定系数法求出直线MA的解析式.
(3)本题要分情况进行讨论:
①当EF∥CA时,△ABC∽△EBF,可根据两直线平行得出直线EF的斜率与直线AC的相同,然后根据直线EF过M点,即可求出直线EF的解析式,然后联立抛物线即可求出它们的交点P的坐标.
②当∠BFE=∠A时,△ABC∽△FBE,思路同①,可通过构建相似三角形来求E点的坐标以得出直线EF的解析式.可过A作AG⊥BC于G,过M作MH⊥AB于H,那么通过相似三角形AGC和MHE可求出E点的坐标,然后同①的方法进行求解即可.
解答: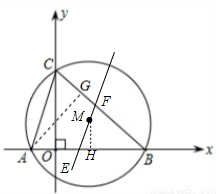 解:(1)由题意可知:A(-1,0),B(3,0),C(0,3)
解:(1)由题意可知:A(-1,0),B(3,0),C(0,3)
可得抛物线的解析式为y=-x2+2x+3
(2)设y轴于圆M的另一交点为D,根据相交弦定理可得出OD=OA•OB÷OC=1
由此可求得M点的纵坐标为1
同理可求出M点的横坐标为1
∴M的坐标为(1,1)
设过A、M点的直线解析式为y=kx+b,有
k+b=1,-k+b=0
∴k= ,b=
,b=
直线解析式为:y= x+
x+
(3)在(1)中的抛物线上存在点P
使△BEF与△ABC相似.
①若△BEF∽△ABC,则EF∥AC
∵直线AC为:y=3x+3
∴设直线EF为:y=3x+b1过m(1,1)
∴直线EF为:y=3x-2
点P的坐标满足y=3x-2,y=-x2+2x+3
解之x1=- +
+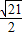 ,x2=-
,x2=- -
-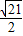
y1=- +
+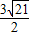 ,y2=-
,y2=- -
-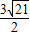
所以P1(- +
+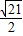 ,-
,- +
+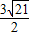 ),P2(-
),P2(- -
-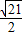 ,-
,- -
-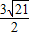 )
)
②若△BEF∽△ABC,则∠ACG=∠MEH
过点A作AG⊥BC于G,有∠AGC=∠MEH
∴△ACG∽△MEH
其中AC=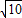 ,CG=
,CG=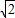 ,AG=2
,AG=2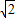 ,MH=1
,MH=1
∵AG:CG=MH:HE,即2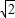 :
: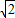 =1:HE
=1:HE
∴HE= ,E的坐标为(
,E的坐标为( ,0)
,0)
直线EM解析式为:y=2x-1
同理可得:P3(2,3),P4(-2,-5)
综上所述:P1(- +
+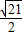 ,-
,- +
+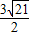 ),P2(-
),P2(- -
-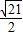 ,-
,- -
-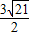 ),P3(2,3),P4(-2,-5).
),P3(2,3),P4(-2,-5).
点评:本题着重考查了待定系数法求二次函数解析式、函数图象的交点、相似三角形的判定和性质等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.
(2)本题的关键是求出M点的坐标,可如果设圆M与y轴的另一交点为D,那么可根据相交弦定理求出OD的长,进而可求出M点的纵坐标,同理可求出M的横坐标,得出M的坐标后可用待定系数法求出直线MA的解析式.
(3)本题要分情况进行讨论:
①当EF∥CA时,△ABC∽△EBF,可根据两直线平行得出直线EF的斜率与直线AC的相同,然后根据直线EF过M点,即可求出直线EF的解析式,然后联立抛物线即可求出它们的交点P的坐标.
②当∠BFE=∠A时,△ABC∽△FBE,思路同①,可通过构建相似三角形来求E点的坐标以得出直线EF的解析式.可过A作AG⊥BC于G,过M作MH⊥AB于H,那么通过相似三角形AGC和MHE可求出E点的坐标,然后同①的方法进行求解即可.
解答:
 解:(1)由题意可知:A(-1,0),B(3,0),C(0,3)
解:(1)由题意可知:A(-1,0),B(3,0),C(0,3)可得抛物线的解析式为y=-x2+2x+3
(2)设y轴于圆M的另一交点为D,根据相交弦定理可得出OD=OA•OB÷OC=1
由此可求得M点的纵坐标为1
同理可求出M点的横坐标为1
∴M的坐标为(1,1)
设过A、M点的直线解析式为y=kx+b,有
k+b=1,-k+b=0
∴k=
 ,b=
,b=
直线解析式为:y=
 x+
x+
(3)在(1)中的抛物线上存在点P
使△BEF与△ABC相似.
①若△BEF∽△ABC,则EF∥AC
∵直线AC为:y=3x+3
∴设直线EF为:y=3x+b1过m(1,1)
∴直线EF为:y=3x-2
点P的坐标满足y=3x-2,y=-x2+2x+3
解之x1=-
 +
+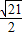 ,x2=-
,x2=- -
-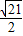
y1=-
 +
+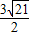 ,y2=-
,y2=- -
-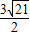
所以P1(-
 +
+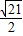 ,-
,- +
+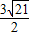 ),P2(-
),P2(- -
-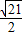 ,-
,- -
-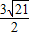 )
)②若△BEF∽△ABC,则∠ACG=∠MEH
过点A作AG⊥BC于G,有∠AGC=∠MEH
∴△ACG∽△MEH
其中AC=
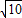 ,CG=
,CG=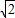 ,AG=2
,AG=2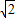 ,MH=1
,MH=1∵AG:CG=MH:HE,即2
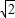 :
: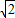 =1:HE
=1:HE∴HE=
 ,E的坐标为(
,E的坐标为( ,0)
,0)直线EM解析式为:y=2x-1
同理可得:P3(2,3),P4(-2,-5)
综上所述:P1(-
 +
+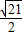 ,-
,- +
+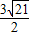 ),P2(-
),P2(- -
-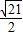 ,-
,- -
-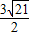 ),P3(2,3),P4(-2,-5).
),P3(2,3),P4(-2,-5).点评:本题着重考查了待定系数法求二次函数解析式、函数图象的交点、相似三角形的判定和性质等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目



 ,梯形的高
,梯形的高 ,且
,且 .
. 时,求作以CF、DF的长为根的一元二次方程.
时,求作以CF、DF的长为根的一元二次方程.