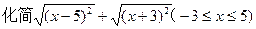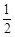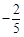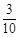题目内容
(本小题满分5分)
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点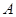 ,测得由点A看树顶端
,测得由点A看树顶端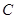 的仰角为35°;
的仰角为35°;
(2)在点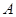 和大树之间选择一点
和大树之间选择一点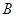 (
(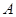 、
、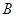 、
、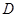 在同一直线上),测得由点
在同一直线上),测得由点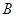 看大树顶端
看大树顶端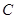 的仰角为45°;
的仰角为45°;
(3)量出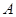 、
、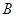 两点间的距离为4.5米.
两点间的距离为4.5米.
请你根据以上数据求出大树CD的高度.(精确到1.0米,参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)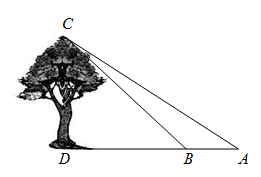
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点
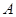 ,测得由点A看树顶端
,测得由点A看树顶端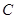 的仰角为35°;
的仰角为35°;(2)在点
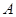 和大树之间选择一点
和大树之间选择一点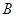 (
(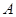 、
、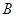 、
、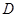 在同一直线上),测得由点
在同一直线上),测得由点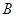 看大树顶端
看大树顶端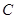 的仰角为45°;
的仰角为45°;(3)量出
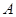 、
、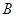 两点间的距离为4.5米.
两点间的距离为4.5米.请你根据以上数据求出大树CD的高度.(精确到1.0米,参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)

10.5
分析:首先分析图形:本题涉及到两个直角三角形△DBC、△ADC,应利用其公共边CD构造等量关系,借助AB=AD-DB=4.5构造方程关系式,进而可求出答案.
解答:解:设CD=x米;∵∠DBC=45°,∴DB=CD=x,AD=x+4.5;
在Rt△ACD中,tan∠A=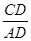 ,∴tan35°=
,∴tan35°=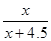 ;解得:x=10.5;
;解得:x=10.5;
所以大树的高为10.5米.
解法2:在Rt△ACD中,tan∠A=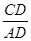 ,∴AD=
,∴AD=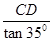 ;
;
在Rt△BCD中,tan∠CBD=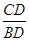 ,∴BD=
,∴BD=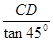 ;
;
而AD-BD=4.5,即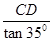 -
-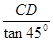 =4.5,
=4.5,
解得:CD=10.5;
所以大树的高为10.5米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:解:设CD=x米;∵∠DBC=45°,∴DB=CD=x,AD=x+4.5;
在Rt△ACD中,tan∠A=
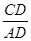 ,∴tan35°=
,∴tan35°=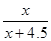 ;解得:x=10.5;
;解得:x=10.5;所以大树的高为10.5米.
解法2:在Rt△ACD中,tan∠A=
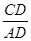 ,∴AD=
,∴AD=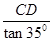 ;
;在Rt△BCD中,tan∠CBD=
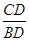 ,∴BD=
,∴BD=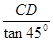 ;
;而AD-BD=4.5,即
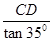 -
-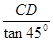 =4.5,
=4.5,解得:CD=10.5;
所以大树的高为10.5米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目

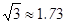 ,结果精确到1 mm)
,结果精确到1 mm)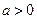 时,如
时,如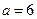 则
则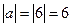 ,故此时
,故此时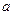 的绝对值是它本身
的绝对值是它本身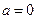 时,
时,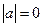 ,故此时
,故此时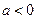 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即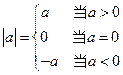
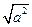 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想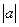 的大小关系.
的大小关系.